Свойства композиции
№1 Надёжность — свойство объекта сохранять во времени в установленных пределах значения всех параметров, характеризующих способность выполнять требуемые функции в заданных режимах и условиях применения, технического обслуживания, хранения и транспортирования. Надёжность как наука развивается в трёх направлениях: Математическая теория надёжности занимается разработкой методов оценки надёжности и изучением закономерностей отказов. Статистическая теория надёжности занимается сбором, хранением и обработкой статистических данных об отказах. Физическая теория надёжности изучает физико-химические процессы, происходящие в объекте при различных воздействиях. №2 Надежность как наука занимается решением таких задач: изучением критериев и количественных характеристик надежности; исследованием методов анализа надежности; разработкой методов испытания оборудования на надежность; разработкой научных методов эксплуатации объектов. №3 Технические средства (элементная база, экспериментальные и производственные возможности) представляют наиболее важную часть активных средств обеспечения безопасности и эффективности сложных технических систем. Уровень технического обеспечения зависит от следующих факторов: - уровней качества и надежности материалов, полуфабрикатов, комплектующих элементов, агрегатов и изделий общего назначения, выпускаемых промышленностью и используемых в составе технических систем; - технического уровня, номенклатуры, производительности, степени автоматизации технических средств для проектирования, отработки производства и эксплуатации сложных изделий; - уровня автоматизации систем и средств оперативного сбора, обработки, обмена информацией для координации и контроля хода создания и применения технических изделий и технологий. Чем сложнее создаваемые технические системы, тем больше в них потенциальных источников отказов, тем проблематичнее становится обеспечение их надежности при достигнутом научно-техническом уровне проектирования, экспериментальной отработки, производства и эксплуатации. Все технические средства обеспечения надежности и безопасности, которые используют при создании и эксплуатации технических систем, могут быть условно разделены на три класса: средства предупреждения, средства контроля и средства защиты. К числу технических средств, используемых для предупреждения отказов конструктивного характера, относят: • автоматизированные цифровые и аналого-цифровые комплексы моделирования, имеющие необходимое математическое обеспечение и позволяющие проектантам разрабатывать большое число альтернативных вариантов элементов системы, режимов их работы и выбирать наиболее надежные и эффективные; • средства автоматизированной разработки конструкторской и технологической документации, позволяющие исключить ошибки в документации и значительно ускорить её разработку; • современное экспериментальное оборудование, позволяющее своевременно отрабатывать новые технические решения, обеспечить высокую надежность элементов; • технические средства обучения и повышения квалификации конструкторов, технологов, экспериментаторов и других сотрудников предприятий-разработчиков; • автоматизированную систему информации по вопросам качества и надежности элементов технических систем. К числу технических средств, предупреждающих отказы и отклонения производственного характера, относят: • прогрессивное автоматизированное производственно-технологическое оборудование, средства контроля и управления технологическими процессами; • технические средства входного неразрушающего контроля и диагностики, исключающие попадание в производство недостаточно качественных материалов, полуфабрикатов и комплектующих элементов; • автоматизированные средства обучения рабочих и инженерно-технических работников предприятий-изготовителей; • автоматизированную систему информации по качеству и надежности систем в производстве. К числу технических средств предупреждения отказов в эксплуатации относят: • технические средства для отработки эксплуатационной документации (стенды, макеты, имитаторы) и обучения эксплуатирующего персонала; • автоматизированные средства контроля, диагностики и поиска неисправностей; • технические средства для проведения предупредительных и регламентных работ. К числу технических средств, обеспечивающих контроль и выявление отказов конструктивного характера, относят: • экспериментальную базу, достаточную для контроля правильности заложенных технических решений, проверки запасов работоспособности элементов во всех режимах функционирования, контроля надежности; • технические средства контроля и корректировки конструкторской документации, качества труда исполнителей. Технические средства контроля надежности в производстве технических систем предназначены для осуществления следующих функций: • проведения эффективного входного, пооперационного и приёмочного контроля качества элементов; • проверки режимов функционирования, запасов работоспособности, проведения контрольно-технологических испытаний; • контроля качества сборки и совместного функционирования групп элементов; • контроля качества технологической документации, стабильности технологических процессов, качества труда исполнителей. Технические средства контроля надежности в эксплуатации: • технические средства неразрушающего контроля и диагностики; • элементов систем, об отказах и неисправностях; • технические средства прогнозирования работоспособности элементов, контроля и поиска неисправностей; • автоматизированные средства контроля качества работы операторов. К числу технических средств защиты, предназначенных для устранения условий возникновения отказов, а также последствий их появления, относят: • технические средства локализации отказов, вводимые непосредственно в состав системы; • технические средства оперативного контроля и управления системой при возникновении опасных ситуаций; • блокировки в ответственных технологических процессах, исключающие возможности разрушения элементов системы при нарушении технологического процесса; В конструкции технических систем для уменьшения ущерба от возможных отказов предусматривают следующие технические средства: - пожаро-взрывобезопасности и пожаротушения; - автоблокировки, исключающие прохождение и выполнение ошибочных команд; - предупреждения ошибочных действий операторов. При разработке новых технических систем в них должны быть включены: - средства предупреждения отказов и отклонений от установленного хода технологических процессов; - средства оперативного контроля и выявления причин отказов и отклонений; - средства защиты от опасных последствий отказов и отклонений. К числу современных средств защиты технических систем от действия опасных отказов относя защитную автоматику. Защитная автоматика - это совокупность организационных и технических средств, используемых в системах для поддержания заданного режима технологического процесса, предотвращения аварийных ситуаций и (или) повреждения элементов систем. Защитная автоматика должна обеспечивать определение состояния оборудования (например, "включено или выключено"), степени его загрузки, режима работы и значений технологических параметров. По функциональному признаку в защитной автоматике выделяют блоки автоматического контроля, измерения, сигнализации, защиты и блокировки. Автоматический контроль и измерения могут проводиться дискретно или непрерывно. В зависимости от места представления показаний различают контроль местный и централизованный (дистанционный). При местном контроле измерительные приборы и индикаторы устанавливаются на объекте контроля, при централизованном, индикаторы выносят на диспетчерский пульт. При контроле предельных положений регистрируются только параметры, соответствующие этим положениям, при непрерывном контроле происходит непрерывное измерение параметров. Сигнализация предназначена для передачи контрольных, управляющих (командных) и информационных сигналов по каналам и линиям связи, например оператору или диспетчеру. Различают сигнализацию предупредительную - для предупреждения персонала о пуске тех или иных механизмов, распорядительную - для пуска и отключения систем оператором, исполнительную - для контроля выполнения распоряжений, аварийную - для оповещения персонала о нарушении нормального хода процессов. Для сигнализации о состоянии распределенных объектов используют телекоммуникацию. Блокировка - совокупность методов и средств, обеспечивающих фиксацию рабочих частей (элементов) технической системы в определенном состоянии (положении), которое сохраняется независимо от того, устранено или нет блокирующее воздействие, чем достигается как безопасность оборудования, так и безопасность обслуживания. №4 Все госстандарты по обеспечению надежность сведены в спец класс 27 и объединены названием: Система стандартов «Надежность в технике» (ССНТ). Структура и состав объектов стандартизации ССНТ:
Еще в годы существования СССР в нашей стране была разработана система стандартов «Надежность в технике» (ССНТ), которая обозначается как ГОСТ 27. В настоящее время ГОСТ 27.001-95 является межгосударственной, региональной системой стандартов стран СНГ. Система стандартов «Надежность в технике» предназначена обеспечить эффективность организационных, конструкционных, технологических и эксплуатационных мероприятий, направленных на достижение оптимального уровня надежности объектов, а также объективность и сопоставимость результатов контроля и испытаний на надежность. В систему стандартов «Надежность в технике» входят технические и организационно-методические стандарты, объекты стандартизации которых относятся к классификационным группам. №5 Техническое состояние – совокупность свойств объекта, характеризующее степень его функциональной пригодности в заданных условиях. Определить техническое состояние – значит выяснить, обладает ли объект набором требуемых свойств, а если не обладает – то по какой причине (это задача технической диагностики). Виды технических состояний: • исправность – неисправность; • работоспособность – неработоспособность; • правильное и неправильное функционирование. Исправность – состояние объекта (системы), в котором он полностью удовлетворяет всем требованиям, установленным в нормативно-технической документации (НТД). Неисправность – состояние объекта, в котором он не соответствует хотя бы одному требованию НТД. Повреждение – событие, состоящее в нарушении исправности. Работоспособность – состояние системы, в котором она в данный момент времени соответствует всем требованиям, установленным в отношении основных параметров, характеризующих нормальное выполнение заданных функций системы. Необходимые требования, по которым определяется работоспособность, должны быть записаны в технической документации на систему. №6 Отказ – событие, состоящее в полной или частичной утрате работоспособности. Отказы могут быть классифицированы по ряду признаков. 1. По степени влияния на работоспособность – полный отказ и частичный отказ. Полный отказ приводит к полному нарушению работоспособности, а частичный вызывает несоответствие системы ряду требований, например, рост динамической ошибки при сохранении величины статической ошибки. 2. По физическому характеру отказа – внезапный (катастрофический отказ), который приводит к скачкообразному изменению параметров элемента, на-пример, обрыв, короткое замыкание и т. д., и постепенный (параметрический), который выражается в медленном изменении параметров (старение, износ; отказ кинескопа). При внезапном отказе процесс перехода системы и работоспособного состояния в неработоспособное происходит за время много меньшее времени работы системы (перегорание лампочки). 3. По связи с другими отказами – независимый отказ, который не является причиной отказа других элементов, и зависимый отказ, который приводит к изменению характеристик надежности других элементов. 4. По времени существования – устойчивый отказ (типа обрыв), временный отказ (сбой, вызванный, например, временным изменением условий эксплуатации и исчезающий (самоустраняющийся) при их нормализации) и перемежающийся отказ – многократно повторяющийся временной отказ, свидетельствующий о не-нормальном режиме работы или эксплуатации. 5. По последствиям – обычные отказы (прекращают функционирование объекта) и аварийные отказы (сопровождаются разрушением объекта и т. д.). 6. По внешнему проявлению – явные отказы и скрытые (трудно обнаруживаемые) отказы, для выявления которых используют специальные средства. 7. По возможности устранения – устранимые и неустранимые. 8. По времени возникновения – на этапе испытания, приработки или нормальной эксплуатации объекта. Для каждой конкретной системы понятие “отказ” и его классификация необходимо детально изучить и конкретизировать, так как в зависимости от этого изменяются способы расчета и обеспечения надежности системы. Наработка на отказ – продолжительность или объем работы объекта до возникновения отказа. Технический ресурс объекта – это его наработка от начала эксплуатации или её возобновления после капитального ремонта до наступления предельного состояния объекта. №7 Свойства надежности: • Безотказность – свойство объекта сохранять работоспособность в течение некоторого времени или вплоть до выполнения объема работы без вынужденных перерывов. • Ремонтопригодность – приспособленность объекта к проведению работ по его обслуживанию и ремонту. • Долговечность – свойство объекта сохранять работоспособность в течение определенного времени или вплоть до выполнения определенного объема работ при условии проведения технического обслуживания. Количественными характеристиками надежности могут быть: • вероятность безотказной работы; • среднее время безотказной работы; • интенсивность отказов; • частота отказов; • различные коэффициенты надежности. № 8 Для невосстанавливаемых потребителем изделий показателями надежности являются: Вероятность безотказной работы P(t) – вероятность того, что при определенных условиях эксплуатации в пределах заданной наработки не произойдет ни одного отказа, т.е. P(t) = P(T>t). Вероятность отказа – вероятность того, что при определенных условиях эксплуатации в пределах заданной наработки возникнет хотя бы один отказ, т.е. Q(t) = P(T ≤ t). Плотность распределения наработки до отказа f(t) – это отношение числа отказавших изделий в единицу времени к первоначальному числу испытываемых изделий при условии, что все вышедшие из строя изделия не восстанавливаются. Интенсивность отказов λ(t) – это отношение числа отказавших изделий в единицу времени к среднему числу изделий, исправно работающих в данный отрезок времени. №9
f(t) – плотность распределения, то есть плотность вероятности случайного события; P(t) – вероятность безотказной работы; l(t) – интенсивность отказов; T1 – средняя наработка до отказа. Наиболее полным показателем надежности при таких испытаниях является плотность вероятности f(t), т.к. она несет информацию о времени безотказной работы. Математические зависимости основных показателей надежности невосстанавливаемых объектов: №10 Долговечность свойство изделия сохранять работоспособность до предельного состояния с необходимыми перерывами для технического обслуживания и ремонтов. Средний ресурс - это математическое ожидание ресурса. Гамма-процентный ресурс – это наработка, в течение которой объект не достигнет предельного состояния с заданной вероятность γ, выраженной в процентах. Назначенный ресурс - суммарная наработка, при достижении которой эксплуатация объекта должна быть прекращена независимо от его технического состояния. Средний срок службы - математическое ожидание срока службы. Гамма-процентный срок службы - календарная продолжительность от начала эксплуатации объекта, в течение которой он не достигнет предельного состояния с заданной вероятностью γ, выраженной в процентах. Назначенный срок службы - календарная продолжительность эксплуатации объекта, при достижении которой применение по назначению должно быть прекращено. Сохраняемость свойство изделия, устройства, сооружения непрерывно сохранять (в заданных пределах) значения установленных для них показателей качества во время и после хранения и при транспортировке. Срок сохраняемости — Календарная продолжительность хранения и (или) транспортирования объекта, в течение которой сохраняются в заданных пределах значения параметров, характеризующих способность объекта выполнять заданные функции. Гамма-процентный срок сохраняемости — срок сохраняемости достигаемый объектом с заданной вероятностью γ, выраженной в %. №11 Случайные величины могут принимать дискретные, непрерывные и дискретно-непрерывные значения. Соответственно случайные величины классифицируют на дискретные, непрерывные и дискретно-непрерывные (смешанные). Случайная величина называется дискретной, если она может принимать конечное или бесконечное счетное множество значений, то есть если эти значения могут быть пронумерованы в каком-нибудь порядке К дискретным случайным величинам относятся данные статистических (эмпирических) наблюдений об отказах объектов — наработка до отказа, число отказов. №12 Для графического изображения ряда накопленных частот используется кумулятивная кривая ряд распределения
№13 Закон распределения случайной величины - соотношение устанавливающие связь между значениями случайной величины и их вероятностями. Гипергеометрический закон распределения. Возможные значения X: 0,1,…,n. И каждому значению X=m соответствует вероятность P(X=m)=P= Биномиальный закон распределения. Случайная величина может принимать значения 0,1,2,…,n и каждому значению X=m соответствует вероятность Пуассоновский закон распределения. Случайная величина имеет возможные значения 0,1,2,3,…… и каждому значению Х=m соответствует вероятность №14 Экспоненциальным распределением называется частный случай гамма-распределения с параметрами Используя свойства два плотности распределения, можно найти функцию распределения Основные характеристики (математическое ожидание и дисперсия) случайной величины Характеристическая функция экспоненциального распределения задаётся формулой Кривая экспоненциального распределения вероятностей показана на рис. 21,а, а график функции распределения
Экспоненциальное (показательное) распределение часто встречается в теории массового обслуживания (например, Нормальный закон распределения (закон Гаусса). Плотность вероятности нормально распределённой случайной величины
Наконец, если
Логарифмически нормальное распределение Говорят, что случайная величина Y имеет логарифмически нормальное распределение (сокращённо логнормальное распределение), если её логарифм lnY=X распределён нормально, то есть если
Математическое ожидание и дисперсию логнормального распределения определяют по формулам
Распределение Вейбула
Математическое ожидание и мода случайной величины, распределённые по закону Вейбула, имеют следующий вид: Распределение Вейбула в ряде случаев характеризует срок службы радиоэлектронной аппаратуры и, кроме того, применяется для аппроксимации различных несимметричных распределений в математической статистике. Распределение хи-квадрат Частный случай гамма-распределения с параметрами Основные хар-ки распределение хи квадрат (матем ожидание и дисперсия):
№15 В математике компози́ция фу́нкций (суперпози́ция фу́нкций) — это применение одной функции к результату другой. Композиция функций G и F обычно обозначается G o F, что означает применение функции G к результату функции F. Пусть
Свойства композиции Композиция ассоциативна: Если То Если Рассмотрим пространство всех биекций множества №16 1. Значения функции распределения вероятностей принадлежат отрезку [0,1]: 0≤F(x)≤1. Следствие. Если возможные значения непрерывной случайной величины расположены на всей числовой оси, то справедливы следующие предельные соотношения:
Свойства плотности распределения вероятностей 1. Плотность распределения вероятностей – неотрицательная функция: f(x)≥0.. Числовые характеристики непрерывных случайных величин Математическим ожиданием непрерывной случайной величины X, возможные значения которой принадлежат отрезку [a, b], называют определенный интеграл
|



 Для оценки основных показателей надежности работы изделия проводятся испытания их, причем методики испытаний зависят от поставленной задачи. Многообразие моделей испытаний можно разбить на две основные. По первой модели испытания считаются законченными, если отказали все Nо испытываемых изделий. При этом испытываются на надежность невосстанавливаемые объекты. Отказавшие изделия не заменяются. В этом случае наиболее удобно пользоваться следующими показателями (для оценки надежности):
Для оценки основных показателей надежности работы изделия проводятся испытания их, причем методики испытаний зависят от поставленной задачи. Многообразие моделей испытаний можно разбить на две основные. По первой модели испытания считаются законченными, если отказали все Nо испытываемых изделий. При этом испытываются на надежность невосстанавливаемые объекты. Отказавшие изделия не заменяются. В этом случае наиболее удобно пользоваться следующими показателями (для оценки надежности): Наиболее простую форму можно придать закону распределения дискретной случайной величины. Рядом распределения дискретной случайной величины называется таблица, в которой перечислены в порядке возрастания все возможные значения случайной величины X: x1, x2, …, xn, … и вероятности этих значений p1, p2, …, pn, …, где pi=P{X=xi} – вероятность того, что в результате опыта СВ Х примет значение xi (i=1,2,…, n, …).
Наиболее простую форму можно придать закону распределения дискретной случайной величины. Рядом распределения дискретной случайной величины называется таблица, в которой перечислены в порядке возрастания все возможные значения случайной величины X: x1, x2, …, xn, … и вероятности этих значений p1, p2, …, pn, …, где pi=P{X=xi} – вероятность того, что в результате опыта СВ Х примет значение xi (i=1,2,…, n, …). . Эта случайная величина, например, равна числу m бракованных изделий среди n взятых наугад из партии объёма N, содержащей M бракованных изделий.
. Эта случайная величина, например, равна числу m бракованных изделий среди n взятых наугад из партии объёма N, содержащей M бракованных изделий. , где p+q=1. Этот закон распределения считается заданным, если известны числа n и p, через которые выражаются все вероятности. Случайную величину подчинённою этому закону можно назвать числом появлении события в n независимых опытах.
, где p+q=1. Этот закон распределения считается заданным, если известны числа n и p, через которые выражаются все вероятности. Случайную величину подчинённою этому закону можно назвать числом появлении события в n независимых опытах. ,где ƛ- некоторый параметр, вероятностный смысл которого будет указан несколько страниц спустя.
,где ƛ- некоторый параметр, вероятностный смысл которого будет указан несколько страниц спустя. , то есть то есть плотность вероятности в этом случае
, то есть то есть плотность вероятности в этом случае 
 экспоненциального закона:
экспоненциального закона: 
 , распределённой по экспоненциальному, имеют вид
, распределённой по экспоненциальному, имеют вид 

 Статистический смысл параметра
Статистический смысл параметра 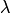 состоит в следующем:
состоит в следующем:  есть средний промежуток времени между двумя последовательными событиями.
есть средний промежуток времени между двумя последовательными событиями.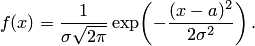 Кривая распределения изображена на рис. 16. Она симметрична относительно точки
Кривая распределения изображена на рис. 16. Она симметрична относительно точки  (точка максимума). При уменьшении
(точка максимума). При уменьшении  ордината точки максимума неограниченно возрастает, при этом кривая пропорционально сплющивается вдоль оси абсцисс, так что площадь под её графиком остаётся равной единицы (рис. 17).
ордината точки максимума неограниченно возрастает, при этом кривая пропорционально сплющивается вдоль оси абсцисс, так что площадь под её графиком остаётся равной единицы (рис. 17). Нормальный закон распределения широко применяется в задачах практики. Объяснить причины этого впервые удалось Ляпунову. Он показал, что если случайная величина может рассматриваться как сумма большого числа малых слагаемых, то при достаточно общих условиях закон распределения этой случайной величины близок к нормальному независимо от того, каковы законы распределения отдельных слагаемых. А так как практически случайные величины в большинстве случаев бывают результатом действия множества причин, то нормальный закон оказывается наиболее распространённым законом распределения. Укажем числовые характеристики нормально распределённой случайной величины (математическое ожидание и дисперсия):
Нормальный закон распределения широко применяется в задачах практики. Объяснить причины этого впервые удалось Ляпунову. Он показал, что если случайная величина может рассматриваться как сумма большого числа малых слагаемых, то при достаточно общих условиях закон распределения этой случайной величины близок к нормальному независимо от того, каковы законы распределения отдельных слагаемых. А так как практически случайные величины в большинстве случаев бывают результатом действия множества причин, то нормальный закон оказывается наиболее распространённым законом распределения. Укажем числовые характеристики нормально распределённой случайной величины (математическое ожидание и дисперсия): Таким образом, параметры
Таким образом, параметры  и
и 
 Эта формула показывает, что нормальный закон распределения полностью определяется математическим ожидание и дисперсией случайной величины. Таким образом, математическое ожидание и дисперсия полностью характеризуют нормально распределённую случайную величину. Разумеется, что в общем случае, когда характер закона распределения неизвестен, знание математического ожидания и дисперсии недостаточно для определения этого закона распределения. Характеристическая функция нормального распределения случайной величины задаётся формулой
Эта формула показывает, что нормальный закон распределения полностью определяется математическим ожидание и дисперсией случайной величины. Таким образом, математическое ожидание и дисперсия полностью характеризуют нормально распределённую случайную величину. Разумеется, что в общем случае, когда характер закона распределения неизвестен, знание математического ожидания и дисперсии недостаточно для определения этого закона распределения. Характеристическая функция нормального распределения случайной величины задаётся формулой 
 , то случайная величина, распределённая по нормальному закону с такими параметрами, называется стандартизированной нормальной величиной. На рис. 18 изображён график плотности вероятности этой величины
, то случайная величина, распределённая по нормальному закону с такими параметрами, называется стандартизированной нормальной величиной. На рис. 18 изображён график плотности вероятности этой величины
 где величина X имеет нормальное распределение с параметрами
где величина X имеет нормальное распределение с параметрами 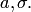 Плотность логнормального распределения задаётся формулой
Плотность логнормального распределения задаётся формулой 

 Логарифмически нормальное распределение встречается в ряде технических задач. Оно даёт распределение размеров частиц при дроблении, содержаний элементов в минералах в извержённых горных пародах, численности рыб в море и т.д. Встречается такое распределение во всех задачах, где логарифм рассматриваемой величины можно представить в виде суммы большого количества независимых равномерно малых величин:
Логарифмически нормальное распределение встречается в ряде технических задач. Оно даёт распределение размеров частиц при дроблении, содержаний элементов в минералах в извержённых горных пародах, численности рыб в море и т.д. Встречается такое распределение во всех задачах, где логарифм рассматриваемой величины можно представить в виде суммы большого количества независимых равномерно малых величин: то есть
то есть  , где
, где  независимы.
независимы. Случайная величина
Случайная величина 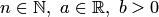 , если её плотность распределения вероятностей записывается в виде
, если её плотность распределения вероятностей записывается в виде


 и
и 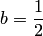 называется распределением хи-квадрат с
называется распределением хи-квадрат с  степенями свободы (пишут
степенями свободы (пишут  ). Если случайная величина
). Если случайная величина 

 и
и  две функции. Тогда их композицией называется функция
две функции. Тогда их композицией называется функция  , определённая равенством:
, определённая равенством: .
. .
. — тождественное отображение на
— тождественное отображение на  , то есть
, то есть  ,
, .
. — тождественное отображение на
— тождественное отображение на  , то есть
, то есть  , то
, то 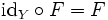 .
.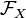 . То есть если
. То есть если  , то
, то  — биекция. Тогда композиция функций из
— биекция. Тогда композиция функций из  — группой.
— группой. 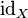 является нейтральным элементом этой группы. Обратным к элементу
является нейтральным элементом этой группы. Обратным к элементу  — обратная функция. Группа
— обратная функция. Группа  .
.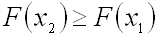 , если
, если  .
. .
. .
. ;
; 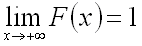 .
. . Следовательно, зная плотность распределения вероятности f(x), можно найти функцию распределения F(x) по формуле
. Следовательно, зная плотность распределения вероятности f(x), можно найти функцию распределения F(x) по формуле .
. . Вероятностный смысл плотности распределения вероятности. Вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу (x, x+∆x), приближенно равна (с точностью до бесконечно малых высшего порядка относительно ∆x) произведению плотности распределения вероятности в точке на длину интервала ∆x:
. Вероятностный смысл плотности распределения вероятности. Вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу (x, x+∆x), приближенно равна (с точностью до бесконечно малых высшего порядка относительно ∆x) произведению плотности распределения вероятности в точке на длину интервала ∆x: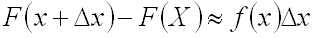 .
. , или
, или 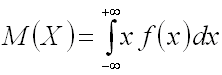 - для всей числовой оси.
- для всей числовой оси.


