Мономолекулярная адсорбция. Изотерма адсорбции Ленгмюра
Чтобы получить теоретическую изотерму адсорбции, описывающую широкую область концентраций, необходимо использование представлений о механизме адсорбции и конкретных моделей. Адсорбция рассматривается как квазихимическая реакция между адсорбатом и адсорбционными центрами поверхности адсорбента. В этом заключается основная идея адсорбционной теории Ленгмюра, которая явилась фундаментальным вкладом в учение об адсорбции. Ограниченность поверхности адсорбента приводит к ее адсорбционному насыщению по мере увеличения концентрации распределяемого вещества. Это положение теории Ленгмюра уточняется следующими допущениями: 1) адсорбция локализована (молекулы не перемещаются по поверхности) на отдельных адсорбционных центрах, каждый из которых взаимодействует только с одной молекулой адсорбата; в результате образуется мономолекулярный слой; 2) адсорбционные центры энергетически эквивалентны – поверхность адсорбента эквипотенциальна; 3) адсорбированныемолекулы не взаимодействуют друг с другом. 4) адсорбция обратима. Для получения уравнения изотермы обратимся к основному положению теории Ленгмюра. Примем, что при адсорбции происходит квазихимическая реакция между распределяемым компонентом и адсорбционными центрами поверхности:
где По мере увеличения концентрации (давления) вещества В реакция сдвигается в сторону образования комплекса и свободных адсорбционных центров становится меньше. Константа адсорбционного равновесия равна
В этом соотношении
где А – величина адсорбции вещества В; A ¥ – емкость адсорбционного монослоя, или число адсорбционных центров, приходящихся на единицу площади поверхности (или на единицу массы адсорбента); А0 – число оставшихся свободными адсорбционных центров, приходящихся на единицу площади поверхности (или на единицу массы адсорбента). Подставляя уравнения (IX.7) в уравнение (IX.6), получим:
Опуская индекс при обозначении концентрации адсорбата СВ , после простых преобразований окончательно имеем:
Выражение (IX.8) называется уравнением изотермы мономолекулярной адсорбции Ленгмюра. Так как концентрации газов и паров практически пропорциональны парциальным давлениям, то для них изотерма адсорбции Ленгмюра принимает вид:
Необходимо отметить, что константа адсорбционного равновесия в уравнении Ленгмюра характеризует энергию взаимодействия адсорбата с адсорбентом. Чем сильнее это взаимодействие, тем больше константа адсорбционного равновесия. Адсорбционное уравнение Ленгмюра часто представляют относительно степени заполнения поверхности – отношения величины адсорбции А к емкости монослоя А¥
Типичная изотерма адсорбции Ленгмюра показана на рис.20.
Рис.20. Изотерма адсорбции Ленгмюра
Важны экстраполяционные следствия из соотношений (IX.8) – (IX.9). При малых концентрациях или давлениях, когда С ® 0, получаем:
Выражения (IX.11) соответствуют закону Генри: величина адсорбции линейно растет с увеличением концентрации. При больших концентрациях и давлениях, когда КC >> 1и KP >> 1, уравнения (IX.8) – (IX.9) переходят в соотношения:
Соотношения (IX.12) отвечают состоянию насыщения, когда вся поверхность адсорбента покрывается мономолекулярным слоем адсорбата. Экспериментальное определение А¥ позволяет рассчитать удельную поверхность адсорбента (поверхность единицы массы адсорбента):
где А¥ -предельная адсорбция, выражаемая числом молей адсорбата на единицу массы адсорбента; N A – число Авогадро; Экспериментальные результаты по определению изотермы адсорбции обычно обрабатывают с помощью уравнения Ленгмюра, записанного в линейной форме (числитель (IX.8) переносят в знаменатель, а знаменатель – в числитель):
Если обе части уравнения (IX.13) умножить на С, то получим ещё одну форму записи указанного уравнения, дающего линейную зависимость в координатах
Такая линейная зависимость позволяет графически определить оба постоянных параметра (А ¥ и К)адсорбционной изотермы. На рис.21 представлена типичная изотерма адсорбции в координатах уравнения (IХ.13а). Экстраполяция зависимости до оси ординат дает отрезок, равный 1/(А ¥ K), а тангенс угла наклона прямой к оси абсцисс равен 1/ А ¥,
Рис.21. Изотерма адсорбции в координатах линейной формы уравнения Ленгмюра (IX.13а) При адсорбции газов из их смесей в соответствии с уравнением изотермы Ленгмюра величины адсорбции суммируются, а концентрация свободных центров A 0 является общей для равновесной многокомпонентной системы. Степень заполнения для i-oго компонента составит:
где Pi – парциальное давление i-oго компонента, а Ki – его адсорбционная константа равновесия. Из уравнения (IX.14) следует, что увеличение парциального давления одного компонента подавляет адсорбцию других, и тем сильнее, чем больше его адсорбционная константа равновесия. Все рассмотренные до сих пор уравнения справедливы для мономолекулярной адсорбции, протекающей на адсорбенте с энергетически эквивалентными адсорбционными центрами. Однако реальные поверхности твердых тел, как правило, не обладают такими свойствами. Для приближения к реальным условиям целесообразно рассмотрение возможных распределений адсорбционных центров поверхности адсорбента по энергиям. Приняв экспоненциальное распределение адсорбционных центров по энергиям, в области средних заполнений получается найденное эмпирически уравнение Фрейндлиха:
где К и п – постоянные. Уравнение Фрейндлиха широко используется при обработке экспериментальных адсорбционных данных, в том числе в инженерных расчётах. Чаще всего оно применяется в логарифмической форме
позволяющей построить линейную зависимость ln A – ln P и графически определить оба постоянных параметра K и п.
|

 ↔
↔ 
 – адсорбционные центры поверхности; В – распределяемое вещество;
– адсорбционные центры поверхности; В – распределяемое вещество;  – комплекс, образующийся на поверхности.
– комплекс, образующийся на поверхности.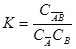 (IX.6)
(IX.6)
 (IX.7)
(IX.7)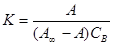
 (IX.8)
(IX.8) (IX.9)
(IX.9) (IX.10)
(IX.10)
 и
и  (IX.11)
(IX.11) и
и 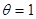 (IX.12)
(IX.12)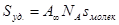 (IX.12a)
(IX.12a)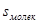 – площадь, занимаемая одной молекулой адсорбата.
– площадь, занимаемая одной молекулой адсорбата.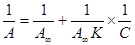 (IX.13)
(IX.13) и С:
и С: (IX.13а)
(IX.13а)
 (IX.14),
(IX.14), (IX.15)
(IX.15)



