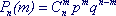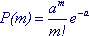Математическое ожидание (среднее значение)

Определение:
Математическим ожиданием называется
- для дискретной случайной величины: (6.4)

Сумма берется по всем значениям, которые принимает случайная величина. Ряд должен быть абсолютно сходящимся (в противном случае говорят, что случайная величина не имеет математического ожидания)

- для непрерывной случайной величины: ; (6.5)

Интеграл должен быть абсолютно сходящимся (в противном случае говорят, что случайная величина не имеет математического ожидания)

 

Свойства математического ожидания:

a. Если С постоянная величина, то МС = С
b. МСх = СМх
c. Математическое ожидание суммы случайных величин всегда равно сумме их математических ожиданий: М(х+y) = Мх + Мy d. Вводится понятие условного математического ожидания. Если случайная величина принимает свои значения х_i с различными вероятностями p(x_i/H_j) при разных условиях H_j, то условное математическое ожидание определяется

как или ; (6.6)

Если известны вероятности событий H_j, может быть найдено полное

математическое ожидание: ; (6.7)

Пример 4: Сколько раз в среднем надо бросать монету до первого выпадения герба? Эту задачу можно решать "в лоб"

xi	1 2 3... k..
p(xi):		,

но эту сумму еще надо вычислить. Можно поступить проще, используя понятия условного и полного математического ожидания. Рассмотрим гипотезы Н₁ - герб выпал в первый же раз, Н₂ - в первый раз он не выпал. Очевидно, р(Н₁) = р(Н₂) = ½; Мx / Н₁ = 1;
Мx / Н₂ на 1 больше искомого полного матожидания, т.к. после первого бросания монеты ситуация не изменилась, но один раз она уже брошена. Используя формулу полного математического ожидания, имеем Мх = Мx / Н₁×р(Н₁) + Мx / Н₂×р(Н₂) = 1×0.5 + (Мх + 1)×0.5, разрешая уравнение относительно Мх, получаем сразу Мх = 2.

e. Если f(x) - есть функция случайной величины х, то определено понятие математического ожидания функции случайной величины:

- для дискретной случайной величины: ; (6.8)

Сумма берется по всем значениям, которые принимает случайная величина. Ряд должен быть абсолютно сходящимся.

-для непрерывной случайной величины: ; (6.9)

Интеграл должен быть абсолютно сходящимся.

2. Дисперсия случайной величины
Определение:
Дисперсией случайной величины х называется математическое ожидание квадрата отклонения значения величины от ее математического ожидания: Dx = M(x-Mx)²

- для дискретной случайной величины: ; (6.10)

Сумма берется по всем значениям, которые принимает случайная величина. Ряд должен быть сходящимся (в противном случае говорят, что случайная величина не имеет дисперсии)

- для непрерывной случайной величины: ; (6.11)

Интеграл должен быть сходящимся (в противном случае говорят, что случайная величина не имеет дисперсии)

Свойства дисперсии:
a. Если С - постоянная величина, то DС = 0
b. DСх = С²Dх
c. Дисперсия суммы случайных величин всегда равно сумме их дисперсий только, если эти величины независимы (определение независимых величин)
d. Для вычисления дисперсии удобно использовать формулу:

Dx = Mx² - (Mx)² (6.12)

Связь числовых характеристик
и параметров типичных распределений

распределение	параметры	формула	Mx	Dx
равномерное	a, b		(b+a) / 2	(b-a)2 / 12
нормальное	a, σ		a	σ2
Бернулли	n, p		np	npq
Пуассона	a		a	a