Билет 7. Политропный процесс - термодинамический процесс, во время которого удельная теплоёмкость c газа остаётся неизменной.
Политропный процесс - термодинамический процесс, во время которого удельная теплоёмкость c газа остаётся неизменной. Для идеального газа уравнение политропы может быть записано в виде: pV^n = const
В зависимости от процесса можно определить значение n:
1. Изотермический процесс: n = 1, так как PV1 = const, значит PV = const, значит T = const. 2. Изобарный процесс: n = 0, так как PV0 = P = const. 3. Адиабатный процесс: n = γ, это следует из уравнения Пуассона. Здесь γ — показатель адиабаты.
Величина n, зависящая от теплоемкости политропного процесса, называется показателем политропы. Будучи постоянным для конкретного процесса, значение показателя политропы может изменяться в зависимости от теплоемкости сп от +оо до —оо и определяет характер процесса. Работа газа в политропическом процессе может быть определена с помощью интеграла при подстановке в него уравнения политропы Интегрирование в выражении дает формулу для определения работы в политропическом процессе
де: и p1 и v1 - начальные давление и объём газа, v2 - его конечный объём. Из этой формулы, в частности, следует, что работа при расширении газа всегда остаётся положительной, независимо от того, какое значение принимает показатель политропы, больше или меньше единицы. Теплоемкость является положительной величиной, если при получении тепла система разогревается и, наоборот, если система, отдавая тепло, охлаждается. Однако теплоемкость может быть и отрицательной. Это, как видно из формулы наблюдается в двух случаях:
1) при получении тепла система охлаждается,
2) при отдаче тепла система разогревается.
В первом случае газ производит работу расширения Во втором случае работа, производимая над газом при его сжатии
Внутренняя энергия системы увеличивается, а значит, ее температура растет, несмотря на то, что газ отдает теплоту. Подобный процесс происходит в некоторых звездах: гравитационные силы при сжатии звезды совершают работу большую, чем излучаемое ей тепло, поэтому звезда разогревается, несмотря на то, что она излучает теплоту. Наконец, обратим внимание на размерность теплоемкости. В системе СИ ее размерностью, как видно из формулы, является
|

 - показатель политропы
- показатель политропы
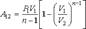

 в количестве большем, чем количество теплоты
в количестве большем, чем количество теплоты  , которое подводится к газу в процессе расширения
, которое подводится к газу в процессе расширения 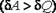 . В этом случае на производство работы помимо тепла, подведенного к газу, расходуется и некоторое количество его внутренней энергии. Хотя к газу и подводится тепло, но оно целиком превращается в работу, а убыль внутренней энергии
. В этом случае на производство работы помимо тепла, подведенного к газу, расходуется и некоторое количество его внутренней энергии. Хотя к газу и подводится тепло, но оно целиком превращается в работу, а убыль внутренней энергии  газа ведет к снижению температуры.
газа ведет к снижению температуры. , оказывается по абсолютной величине большей, чем количество отдаваемого им тепла. С учетом знаков количества теплоты
, оказывается по абсолютной величине большей, чем количество отдаваемого им тепла. С учетом знаков количества теплоты  и работы
и работы  равенство принимает вид:
равенство принимает вид:




