Менеджер по продажам/ менеджер экспортных проектов
· Формула Эйлера. Пусть
Если число
Если число
Таким образом, имеем равенство
которое называется формулой Эйлера. · Показательная форма записи комплексного числа. Рассмотрим произвольное комплексное число, записанное в тригонометрической форме:
а тогда
Следовательно, любое комплексное число можно представить в так называемой показательной форме:
·
Log [ r (cosj + i sinj)] = x + yi равносильно следующему:
ex+yi = r (cosj + i sinj). Последнее равенство можно написать так:
ex(cos y + i sin y) = r (cosj + i sinj), откуда, сравнивая модули и аргументы, получим:
ex = r, y = j + 2kp (k = 0, ±1, ±2,...), т.е.
x = log r и x + yi = log r + (j + 2kp)i и окончательно
т.е. натуральный логарифм комплексного числа равен комплексному числу, вещественная часть которого есть обычный логарифм модуля, а мнимая часть представляет собою произведение i на одно из значений аргумента.
Возведение комплексных чисел в комплексную степень базируется на простой формуле a^b=exp(b ln a) Экспоне́нта — показательная функция Менеджер по продажам/ менеджер экспортных проектов Компания-работодатель:Агентство бизнес-коммуникаций DIRECT. Направление деятельности - экспортное сопровождение. География деятельности - восемнадцать стран. Руководитель компании – Наталья Подгорецкая, действительный член и руководитель комитета по развитию экспорта и импорта в Санкт-Петербургском отделении общественной организации «Деловая Россия».
|

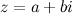 - некоторое комплексное число. По определению полагают, что
- некоторое комплексное число. По определению полагают, что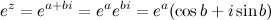
 - действительное, то есть
- действительное, то есть 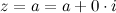 , то
, то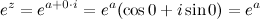
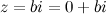 , то
, то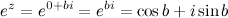
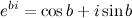
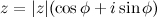 . По формуле Эйлера
. По формуле Эйлера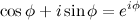
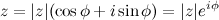
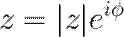
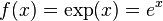 , где е — Число Эйлера (
, где е — Число Эйлера (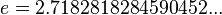 ).
).


