Классификация систем массового обслуживания
Системы, в которых, с одной стороны, возникают массовые запросы (требования) на выполнение каких-либо видов услуг, а, с другой стороны, происходит удовлетворение этих запросов, называются системами массового обслуживания.
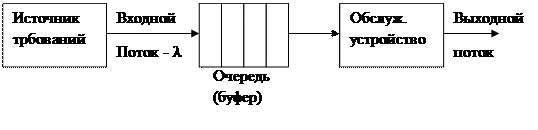
Система массового обслуживания включает следующие элементы: источник требований, входящий поток требований, очередь, обслуживающее устройство (обслуживающий аппарат, канал обслуживания), выходящий поток требований.
Системы массового обслуживания классифицируют по разным признакам. Одним из признаков является ожидание требования начала обслуживания. В соответствии с этим признаком системы подразделяются на следующие виды: 1) системы массового обслуживания с потерями (отказами); 2) системы массового обслуживания с ожиданием; 3) системы массового обслуживания с ограниченной длиной очереди; 4) системы массового обслуживания с ограниченным временем ожидания.
Источник требований: 1. Бесконечный 2. Конечный
Входной поток: 1. Пуасона 2. Эрланга 3. Регулярный По числу каналов обслуживания делятся на одноканальные и многоканальные.
По месту нахождения источника требований СМО делятся на разомкнутые, когда источник находится вне системы, и замкнутые, когда источник находится в самой системе. К последнему виду относится, например, станочный участок, в котором станки являются источником неисправностей, а следовательно, и требований на их обслуживание.
Одной из форм классификации систем массового обслуживания является кодовая (символьная) классификация Д. Кендалла. При этой классификации характеристику системы записывают в виде трех, четырех или пяти символов, например А | B | C | D, где А – тип распределения входящего потока требований, В – тип распределения времени обслуживания, C – число каналов обслуживания. D – количество мест в очереди. Также Запись М | М | 3 означает, что входящий поток требований пуассоновский (простейший), время обслуживания распределено по экспоненциальному закону, в системе имеется три канала обслуживания.
Лекция № 8 (27.09.2013)
Уравнение Колмогорова для вероятностей состояний. Системы, представляемые в виде непрерывной цепи Маркова, обычно исследуют с помощью уравнения Колмогорова для вероятностей состояний. Состояние системы – связано с числом заявок системы.
Плотностью вероятности перехода из состояния в состоянии называется предел отношения вероятности этого перехода за время к длине промежутка, когда последний стремится к нулю:
где - вероятность того, что система, находившаяся в момент в состоянии за время перейдет в состояние. Марковская непрерывная цепь называется однородной, если плотность вероятностей не зависит от времени, в противном случае она называется неоднородной.
Вершины – состояния системы. Дуги – переходы с соответствующих вершин. – система дифф. Уравнения Колмагорова. - уравнение нормировки.
Для однородных Марковских непрерывных цепей, характеризующих процессы гибели и размножения, уравнения Колмогорова имеют вид:
где - вероятность состояния, когда в системе находится требований в момент времени; - общее число возможных состояний В левой части стоит производная вероятности i-го состояния по времени. В правой части записывается сумма произведений вероятностей состояний из которых ведут стрелки в данное состояние на интенсивность соответствующего перехода. Минус произведение вероятности данного i-го состояния на сумму интенсивностей выводящих из этого состояния.
Пример:
;
При стационарном случае система уравнений Колмагорова переходит в систему алгебраических уравнений, которая позволяет определить вероятности. В большинстве практических задач оказывается допустимой гипотеза о стационарном режиме работы системы. Система рождения и гибели:
Используя уравнения Колмагорова получили:
Многофункциональная СМО с отказами (задача Эрланга)
СМО с отказами является такая система, в которой приходящие для обслуживания требования, в случае занятости всех каналов обслуживания, сразу ее покидают. - интенсивность входного потока; - интенсивность обслуживания; - колличество каналов; – среднее число занятых каналов; – относительная пропускная способность (доля обслужанных заявок); - абсолютная пропускная способность (интенсивность потока на выхода); – вероятность потерь;
1. Введем множество состояний – cистема пуста; – один канал занят; – все каналы заняты;
2.
3. Используя формулу гибели и рождения получим – загрузка СМО (вероятность того, что систма находиться в занятом состоянии) ; ; ; ; где ; ; ;
Лекция № 9 (01.10.13) Пример: найти оптимальное число телефонных номеров на предприятии, если заявки на переговоры поступают с интенсивностью в 1/минуту. Среднее время обслуживания (время одного разговора) Найти вероятность того, что в СМО за минуты поступит заявки и не более заявок. При условии, что заявок обслуживаются. ; ;
Видимо расчет таблицы: ;
=;
Одноканальная СМО с отказами.
1. Введем множество возможных состояний – cистема пуста; – система обслуживает заявку;
2. Нарисуем граф состояний
3. Запишем дифференциальное уравнение Колмогорова. ;
– Вероятность того, что СМО находиться в состоянии; – Вероятность того, что СМО находиться в состоянии; – вероятность обслуживания заявки()
Всегда ли существуют финальные вероятности? 1. Финальные вероятности существуют в том случае, если загрузка системы меньше для одноканальной СМО. 2. Число состояний СМО – должно быть конечно и из каждого состояния можно попасть в любое другое состояние за конечное число шагов. Если выполняются оба условия, то можно составить систему Колмогорова. Относительная пропускная способность:; Абсолютная пропускная способность:;
Пример: найти оптимальное число телефонных номеров на предприятии, если заявки на переговоры поступают с интенсивностью в 1/минуту. Среднее время обслуживания (время одного разговора) Определить характеристики СМО и оценить эффективность работы. ; ;
Одноканальная СМО с ограниченной длиной очереди. M/M/3/m 3 – число каналов; m – длина очереди;
СМО с ограниченной длиной очереди является такая система, в которой требование, поступающее на обслуживание, покидает систему, если заняты все каналы обслуживания, и в накопителе заняты все места.
1. Введем множество состояний – cистема пуста; – система обслуживает заявку; – канал занят заявкой + одна заявка в очереди; – канал занят заявкой + m заявок в очереди; 2. Зарисуем граф состояний.
3. Используя формулы гибели и размножения, имеем: ; ; ; ; При условии, что, получим систему без очереди ; Вероятность того, что заявка получит обслуживание – это все остальные вероятности. ; ; ; – размер очереди.) – количество каналов; Очередь будет отдичаться от общего числа заявок в системе на величину звгрузки; Временные характеристики определяются по формуле Литтла: ; ;
1. Введем множество состояний – cистема пуста; – система обслуживает заявку; – n заявка; – канал занят заявкой + n заявок в очереди;
2.
3. Используя формулы гибели и размножения, имеем: ; ; ;
Лекция № 10 (4.10.2013)
; ; – длина очереди. – среднее число заявок, находящихся в системе. – среднее время, которое заявка проводит в очереди. – время пребывания, с момента захода до выхода – время ответа. Вывод формулы Литтла.
- случайный процесс прихода заявок. Поток ординарный в каждый момент времени. - случайный процесс ухода заявок. Система простаивает в момент времени, где ступни кривых совпадают. ; Среднее число заявок на интервале: ; ; Следовательно: – первая формула Литтла. - вторая формула Литтла.
1. Множество состояний – cистема пуста; – один канал занят; – n каналов заняты; – n каналов заняты + 1 заявка в очереди; – n каналов заняты + m заявок в очереди (в этом состоянии происходят потери); 2. Граф состояний
3. Используя формулы рождения и гибели получим: ; ; ; ; ; Вероятность возникновения очереди: ; ; Относительная пропускная способность:; - абсолютная пропускная способность. Среднее число заявок в очереди: ; Среднее число обслуживающих заявок: ; ; По формуле Литла определяем: ; ;
1. Множество состояний. – cистема пуста; – один канал занят; – n каналов заняты; – n каналов заняты + 1 заявка в очереди; – n каналов заняты + 2 заявок в очереди; 2.
3. Используя формулы рождения и гибели получим: ; ; ; ; ; Вероятность образования очереди: ; ; ; Средняя длина очереди. ; ;
Пример: На замок демонов в среднем нападают 3 отряда немцев в час. Замок обороняют колдуна 2-го уровня. Среднее время уничтожения отрядов – час. В очереди подраться могут стоять не более 4 отрядов.
Рещение: ,,. ,, Вероятность отсутствия машин на складе: ; Значит колдуны молодцы но сражаются почти без отдыха. По формуле находим вероятность отказа в атаке замка каким-то отрядом: ; ; Вероятность отказа не столь велика. Относительная пропускная способность равна: ; Среднее число отрядов в очереди находим: ; И это намного меньше 4х
Пример: Интенсивность потока посетителей столовой составляет 150 человек в час () есть кассира () каждый из которых обслуживает человека в минуту. Нацти характеристики СМО.
Решение: ,,. . Вероятность отсутствия посетителей в столовой ; Т.е. работники столовой почти всегда заняты Вероятность образования очереди: ; Среднее число посетителей: человека А среднее число обслуженных посетителей равно: человек Значит ; Т.е. чуть больше одного посетителя на каждого кассира, что оптимально. Среднее время,затрачиваемое посетителями на получение обеда: мин Можно сделать вывод, что работа в столовой организована эффективно.
Лекция № 11 (08.10.2013) СМО с ограниченной очередью и ограниченным временем ожидания. Такие системы, когда в процессе ожидания снижается приоритет заявки. Такая же многоканальная система с отличием – время ожидания в очереди каждого требования ограничено случайной величиной. - предельно допустимое время ожидания. - среднее время ожидания – случайная велмчина, распределенная по экспоненциальному закону. Величина, обратная среднему времени ожидания, означает среднее количество требований, покидающих очередь в единицу времени, вызванное появлением в очереди одного требования:; - среднее число требований, покидающих систему необслуженными, приходящиеся на среднюю скорость обслуживания требований.
1. Введем множество состояний – cистема пуста; – одна заявка; – n заявок; ; – n заявок + m заявок в очереди; 2. Граф состояний
Интенсивность покидания системы зависит от того, что это за заявка и сколько она простояла в очереди. Интенсивность покидания пропорционально месту в очереди.
3. Используя формулы рождения и гибели получим: ; ; ; ; ;
; ;
Вероятность образования очереди: ; Отказ системы происходит в состоянии ;
; ;
СМО замкнутого типа. В замкнутых системах массового обслуживания источник требований находится внутри системы, и интенсивность потока требований зависит от состояния самой системы. Чаще всего потоком требований в такой системе является поток неисправностей от некоторой группы работающих устройств. Пусть имеется работающих устройств, которые могут выходить из строя за счет неисправностей. Имеется также приборов (каналов) обслуживания этих требований. В качестве таких каналов могут выступать и люди. Обычно предполагают, что.
1. Введем множество состояний – cистема пуста; – 1 элемент сломался и ремонтируется; – 2 элемента сломались, 1 ремонтируется, 1 в очереди; – n элементов сломались, 1 ремонтируется, в очереди;
2. Граф состояний
3. Используя формулы рождения и гибели получим:
; ; ; ; ; Когда источник заявок ограничен, то в системе существует статический режим и очередь ограничена. Обслуживание не всегда является экспоненциальным.
Системы типа M//1, M/D/1, M/G/1. Все эти системы имеют решение. Есть формула, которая позволяет вычислить характеристики систем. В результате использования метода вложенных цепей Маркова была получена формула Поллачека-Хинчина: ; – среднее число заявок в очереди и на обслуживание. – среднеквадратическое отклонение. – среднее время обслуживания. – коэффициент вариации времени обслуживания. – время пребывания; – время ожидания; Для другого типа потока формула не выведена. Но мы можем использовать методы диапазонной аппроксимации. 1. Система типа M/D/1 с постоянным обслуживанием. ; 4. Система типа M/M/1 с экспоненциальным обслуживанием. ;; 5. Система типа M//1 с эрланговским обслуживанием. ; – показатель закона Эрланга. ;
Получение проектированного результата при условии, что оценки худшие.
Лекция № 12 (11.10.2013)
Системы с неограниченными потоками.
FIFO – первым пришел, первым обслужился. LIFO – последним пришел, первым обслужился. RANDOM – случайный выбор из очереди. Все потоки равноправны – время ожидания в очереди у них одинаково.
– среднее значение времени обслуживания. – коэффициент вариации времени обслуживания. (отношение времени обслуживания к среднему математическому ожиданию времени обслуживания). – среднее время ожидания в очереди для заявок k-го потока. – среднее время обслуживания заявки, находящейся в приборе в момент прихода помеченной заявки. ; ; Где;
При выводе формулы применяются следущие допущения: 1. Один обслуживающий прибор; 2. Бесконечная очередь; 3. Заявки поступают независимо друг от друга; 4. ДО подчинена произвольному закону и не зависят друг от друга; 5. Прибор обслуживания не простаивает если накопителе имеется хотя бы одна заявка любого класса; 6. Выбор на обслуживание производится мгновенно;
Для без приоритетной дисциплины обслуживания заявки разных классов выбираются на обработку только в зависимости от времени поступления. При использовании приоритетов назначаются по принципу – класс с меньшим номером имеет более высокий приоритет. При использовании дисциплины с абсолютным приоритетом, заявка, обслуживание которой было прервано возвращается в очередь, где ожидает дальнейшего обслуживания, а ее обслуживание начинается с прерванного места. - суммарная загрузка по всем потокам.;
Свойство ДО без приоритетов: 1. Среднее время ожиданий заявок разных классов для бесприоритетной дисциплины одинаково при любых и прилюбых законах распределения длительности обслуживания. 2. Среднее время пребывания в системе заявок разных классов различно, т.к. время пребывания: (- одинаково, - различно) 3. Среднее время ожидания минимальнл когда имеется постоянное, детерминированное время обслуживания и увеличивается с ростом коэффициент вариации. 4. Среднее время ожидания нелинейно зависит от коэффициента вариации (). При получаем; При получаем двухкратное увеличение; При получаем 5 пятикратное увеличение; 5. Среднее время ожидания хаявок зависит от суммарной загрузки систем
, – это превышение относительно равно времени обслуживания. (– различно, - одинаково) длины очередей будут различны. Длины очередей равны если 6. Показано, что если обслуживание производится в обратном порядке(LIFO?) средние времена будут одинаковы, но дисперсия.
Циклическая ДО.
Сперва выбираются заявки из первого потока, далее из второго и так по циклу.
Дисциплины с относительным приоритетом.
6 – обслуживается, 1,2,5,4 – в очереди, 1- только прибыла в очередь. ; Заявки в очереди не мешают обслуживанию заявки. После того как ушла, то меняются приоритеты и выбирается 1. Если в процессе обслуживания пришла еще, то она берется после освобождения. Этот цикл без прерывания. ; Где; ; При анализе зависимости можно сказать, что введение приоритетных заявок приводит к уменьшению времени ожидания высокоприоритетных заявок и увеличению низкоприоритетных заявок. ; ; При использовании ДО с относительными приоритетами, среднее время ожидания монотонно увеличивается при любых интенсивностях и временах обслуживания. ;; ; Для среднего времени пребывания заявок разных классов; может не выполняться.
Введение приоритетов – защита от перегрузок для высокоприоритетных заявок. На рисунке выше изображено характеристика поведения времени ожидания в зависимости от загрузки. При когда все ресурсы системы заняты, возможно обслуживание заявок приоритета.
Лекция №13 (15.10.2013) ДО с абсолютным приоритетом. Иногда нужно уменьшить количество заявок больше чем позволяет относительный приоритет. Для этого используют ДО с абсолютным приоритетом. Допустим, что на обслуживании находится заявка второго приоритета. Если приходит заявка первого приоритета, то они меняются местами и вторая заявка встает в очередь прерванных заявок. Прерванная заявка может обслуживаться либо с начала (мы не рассматриваем) либо с того момента, когда ее прервали.
; – сумма загрузок до k-го ; ; – Среднее время ожидания начала обслуживания; – Среднее время ожидания в прерванном состоянии (время в очереди прерываний); Время ожидания заявок класса зависит только от значений заявок и более приоритетных. Для заявок первого класса, имеющих самый высокий приоритет обеспечивается минимальное время ожидания по сравнению с другими дисциплинами обслуживания. Среднее время ожидания монотонно увеличивается с уменьшением приоритета. Однако время ожидания высокоприоритетных заявок в прерванном состоянии может быть, если. Введение абсолютных приоритетов приводит к уменьшению среднего времени ожидания самых высокоприоритетных заявок и к увеличению других классов. На рисунке изображена зависимость среднего времени k-го класса от номера приоритета.
При проектировании нужно быть осторожным и только в самых необходимых случаях назначать абсолютные приоритеты. В реальной жизни используются смешанные приоритеты.
Закон сохранения времени ожидания. Сумма произведений загрузок i-го потока есть величина постоянная для любой дисциплины обслуживания. ; ; ;
Закон сохранения времени ожидания выполняется при: 1. Система работает без потерь; 2. Система простаивает лишь в том случае, если нет заявок; 3. При наличии прерываний длительность обслуживания прерванных заявок распределена по экспоненциальному закону; 4. Все получающие потоки заявок – простейшие и длительность не зависит от интенсивности обслуженных заявок; Закон сохранения для времени пребывания: ; Изменение дисциплины обслуживания приводит к изменению времени ожидания и прерывания. – времена обработки всех заявок одинаковые. Тогда: ; Частный случай закона гласит, что суммарная длина очередей в обслуживании постоянна.
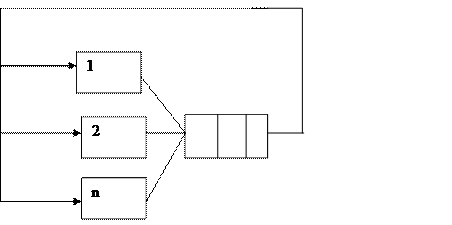
Стохоастические сети СМО. 1. Разомкнутые – есть поток из вне. 2. Замкнутые
Первое предположение: разомкнутая сеть содержит узлов (СМО) Второе предположение: после завершения обслуживания в узле k-я заявка переходит в другой узел. Третье предположение: Все каналы идентичны, заявка может обслуживаться в любом канале. Четвертое предположение: В любомканале есть накопитель бесконечного объема Пятое предположение: Заявки поступают из внешнего источника бесконечной емкости и образуют простейший поток Шестое предположение: Длительность обслуживания экспоненциальная величина распределенная по случайному закону. Седьмое предположение: Прибор не простаивает если есть хоть одна заявка. Задается: 1. – Сколько узлов в сети; 2. – Количество каналов; 3. – Интенсивность обслуживаия СМО 4. Интнсивность входного потока. 5. Матрица-вероятности переходов
Вероятность того, что после тогокак закончиться обслуживание заявки в и перейдет в.
|



 Пусть, тогда
Пусть, тогда

 Нарисуем граф
Нарисуем граф

 - вероятность отказа ()
- вероятность отказа ()

 Формула Литтла связывает 3 величины:
Формула Литтла связывает 3 величины: Одноканальная СМО с неограниченной очередью.
Одноканальная СМО с неограниченной очередью. Зарисуем граф состояний.
Зарисуем граф состояний. ;
;

 Многоканальное СМО с ограниченной очередью.
Многоканальное СМО с ограниченной очередью.
 Многоканальная СМО с неограниченной очередью.
Многоканальная СМО с неограниченной очередью. Граф состояний
Граф состояний






 Входные потоки пуассоновские. Очередь бесконечная. Обслуживание – произвольное.
Входные потоки пуассоновские. Очередь бесконечная. Обслуживание – произвольное.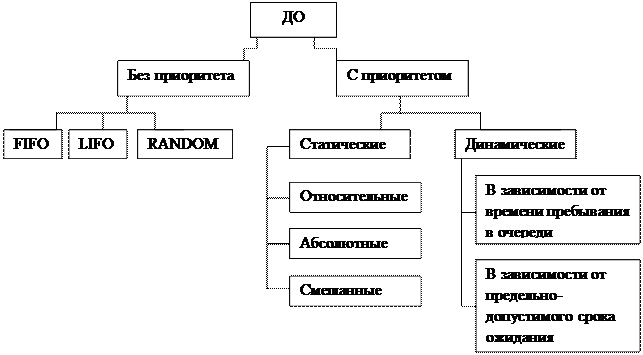 Дисциплина обслуживания(ДО) – порядок выбора заявок из очереди на обслужмвание. Можно предположить множество ДО.
Дисциплина обслуживания(ДО) – порядок выбора заявок из очереди на обслужмвание. Можно предположить множество ДО.


 Приоритет называется относительным, если он учитывается только в момент выбора заявок из очереди на обслуживание и не рказывают влияние на работу системы в период обслуживания заявки любого типа.
Приоритет называется относительным, если он учитывается только в момент выбора заявок из очереди на обслуживание и не рказывают влияние на работу системы в период обслуживания заявки любого типа.








