Для малых выборок найти точечные оценки 1. Выборочное среднее 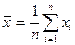 и 2. Выборочная дисперсия
и 2. Выборочная дисперсия  . Исправленная выборочная дисперсия является состоятельной и несмещенной оценкой генеральной дисперсии и вычисляется по формуле
. Исправленная выборочная дисперсия является состоятельной и несмещенной оценкой генеральной дисперсии и вычисляется по формуле 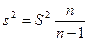 . 3. Исправленное выборочное среднее квадратическое отклонение
. 3. Исправленное выборочное среднее квадратическое отклонение  .
.
Для большой выборки сначала составим группированный статистический ряд. Найдем крайние элементы выборки: 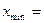 и
и  . Разобьем полученный промежуток на
. Разобьем полученный промежуток на  равных интервалов, вычислив
равных интервалов, вычислив  по формуле Старджесса
по формуле Старджесса 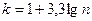 . Для
. Для  =100 получится
=100 получится  =8. Найдем длину каждого интервала
=8. Найдем длину каждого интервала 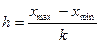 = Границы интервалов определим по формуле
= Границы интервалов определим по формуле  . Во всех вычислениях сохранять 3 знака после запятой. Подсчитаем интервальные частоты:
. Во всех вычислениях сохранять 3 знака после запятой. Подсчитаем интервальные частоты: 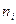 - число элементов выборки, попавших в интервал
- число элементов выборки, попавших в интервал 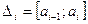 . Элемент выборки, находящийся на границе интервалов, будем относить к правому интервалу.
. Элемент выборки, находящийся на границе интервалов, будем относить к правому интервалу. 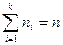 . Значения всех элементов выборки, попавших в интервал
. Значения всех элементов выборки, попавших в интервал 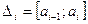 , будем считать равными координате середины интервала
, будем считать равными координате середины интервала 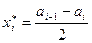 .В таблице приведем результаты первичной обработки статистических данных.
.В таблице приведем результаты первичной обработки статистических данных.
Номер интервала
| Границы интервала
| Частоты
| Относительные частоты
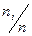
| Приведенные частоты

| Середина интервала
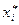
| Ординаты точек кривой Гаусса
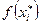
|

| 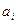
|
| | | | | | | | |
Выборочное среднее:  Исправленное выборочное среднее квадратическое отклонение:
Исправленное выборочное среднее квадратическое отклонение: 
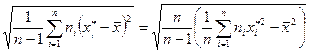
Построим гистограмму приведенных частот  На одном чертеже с гистограммой построим кривую Гаусса для генеральной совокупности
На одном чертеже с гистограммой построим кривую Гаусса для генеральной совокупности 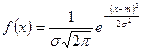 , заменив неизвестные значения генерального среднего
, заменив неизвестные значения генерального среднего 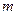 и генерального среднего квадратического отклонения
и генерального среднего квадратического отклонения 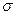 их оценками
их оценками  и
и 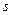 . Ординаты точек кривой Гаусса
. Ординаты точек кривой Гаусса 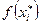 можно вычислить, используя таблицу значений функции
можно вычислить, используя таблицу значений функции  (Гмурман, приложение 1):
(Гмурман, приложение 1): 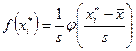 . На том же чертеже построим график плотности равномерного распределения
. На том же чертеже построим график плотности равномерного распределения 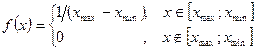 Построить доверительные интервалы
Построить доверительные интервалы  для неизвестного значения генерального среднего
для неизвестного значения генерального среднего 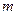 и исследовать зависимость интервальных оценок от объема выборки
и исследовать зависимость интервальных оценок от объема выборки  и доверительной вероятности
и доверительной вероятности 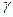 .
. 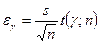 - точность интервальной оценки.
- точность интервальной оценки. 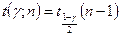 - квантиль порядка
- квантиль порядка 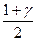 для распределения Стьюдента с
для распределения Стьюдента с  степенью свободы. Таблица
степенью свободы. Таблица 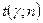 находится в приложении 3 книги Гмурмана.
находится в приложении 3 книги Гмурмана.
Сравнить доверительные интервалы для одинаковой доверительной вероятности  0,95 и разных объемов выборки
0,95 и разных объемов выборки  =10 и
=10 и  =100.
=100.
Сравнить доверительные интервалы для различных доверительных вероятностей  0,95;
0,95;  0,99 и
0,99 и  0,999 и одинаковых объемов выборки
0,999 и одинаковых объемов выборки  =100.
=100.

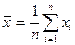 и 2. Выборочная дисперсия
и 2. Выборочная дисперсия  . Исправленная выборочная дисперсия является состоятельной и несмещенной оценкой генеральной дисперсии и вычисляется по формуле
. Исправленная выборочная дисперсия является состоятельной и несмещенной оценкой генеральной дисперсии и вычисляется по формуле 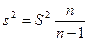 . 3. Исправленное выборочное среднее квадратическое отклонение
. 3. Исправленное выборочное среднее квадратическое отклонение  .
.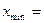 и
и  . Разобьем полученный промежуток на
. Разобьем полученный промежуток на  равных интервалов, вычислив
равных интервалов, вычислив 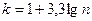 . Для
. Для  =100 получится
=100 получится 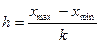 = Границы интервалов определим по формуле
= Границы интервалов определим по формуле  . Во всех вычислениях сохранять 3 знака после запятой. Подсчитаем интервальные частоты:
. Во всех вычислениях сохранять 3 знака после запятой. Подсчитаем интервальные частоты: 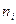 - число элементов выборки, попавших в интервал
- число элементов выборки, попавших в интервал 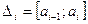 . Элемент выборки, находящийся на границе интервалов, будем относить к правому интервалу.
. Элемент выборки, находящийся на границе интервалов, будем относить к правому интервалу. 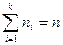 . Значения всех элементов выборки, попавших в интервал
. Значения всех элементов выборки, попавших в интервал 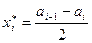 .В таблице приведем результаты первичной обработки статистических данных.
.В таблице приведем результаты первичной обработки статистических данных.
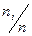

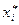
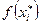

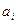
 Исправленное выборочное среднее квадратическое отклонение:
Исправленное выборочное среднее квадратическое отклонение: 
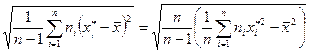
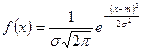 , заменив неизвестные значения генерального среднего
, заменив неизвестные значения генерального среднего 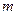 и генерального среднего квадратического отклонения
и генерального среднего квадратического отклонения 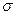 их оценками
их оценками  и
и 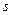 . Ординаты точек кривой Гаусса
. Ординаты точек кривой Гаусса  (Гмурман, приложение 1):
(Гмурман, приложение 1): 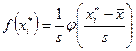 . На том же чертеже построим график плотности равномерного распределения
. На том же чертеже построим график плотности равномерного распределения 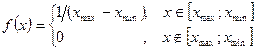 Построить доверительные интервалы
Построить доверительные интервалы  для неизвестного значения генерального среднего
для неизвестного значения генерального среднего 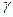 .
. 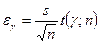 - точность интервальной оценки.
- точность интервальной оценки. 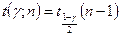 - квантиль порядка
- квантиль порядка 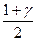 для распределения Стьюдента с
для распределения Стьюдента с  степенью свободы. Таблица
степенью свободы. Таблица 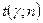 находится в приложении 3 книги Гмурмана.
находится в приложении 3 книги Гмурмана. 0,95 и разных объемов выборки
0,95 и разных объемов выборки 


