Корреляционный анализ. В корреляционном анализе зависимость между случайными величинами изучается с помощью выборочных оценок генеральных коэффициентов корреляцииВ корреляционном анализе зависимость между случайными величинами изучается с помощью выборочных оценок генеральных коэффициентов корреляции. Исследуем зависимость между случайными величинами Построим оценки генерального корреляционного момента Для нормальной генеральной совокупности генеральный коэффициент корреляции равен нулю тогда и только тогда, когда компоненты случайной величины независимы. Поэтому проверка гипотезы о независимости компонент .
|
на основе двумерной выборки 
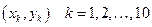. Абсциссы элементов выборки определяются элементами первой малой выборки, упорядоченными по возрастанию. Ординаты элементов выборки определяются элементами второй малой выборки, упорядоченными по возрастанию, как полагается для четных вариантов домашнего задания.
и генерального коэффициента корреляции 
. Согласно методу аналогии, такими оценками будут выборочный корреляционный момент 
и выборочный коэффициент корреляции 
Значения выборочного коэффициента корреляции также как генерального коэффициента корреляции принадлежат отрезку 
.
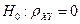против альтернативной гипотезы 
. Известно, что в случае справедливости основной гипотезы статистика 
распределена по закону Стьюдента с 
степенями свободы. Принимая за уровень значимости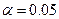 
, найти критическую точку. 
. Сделать выводы о принятии гипотез.
