Оптимальная линейная фильтрация детерминированных и случайных сигналов
Основная статья: Солнечная интерференция При приближении Солнца к оси спутника-наземная станция радиосигнал, принимаемый со спутника наземной станцией, искажается в результате интерференции.
Глава 5 Основы теории оптимальной фильтрации Оптимальная линейная фильтрация детерминированных и случайных сигналов Задачей фильтрации является: - получение из смеси сигнала и шума полезного сигнала в целом. При этом критерием оптимальности может служить минимальное искажении формы (спектра) сигнала; - воспроизведение параметров сигнала несущего информацию. При этом критерием оптимальности может служить максимальное отношение сигнал/шум на выходе линейного фильтра или коррелятора. Различают следующие виды фильтрации: 1. Линейную фильтрацию (сложение, усиление, дифференцирование, интегрирование и т.д.). Здесь выходной сигнал описывается линейными дифференциальными уравнениями. Основным свойством линейной фильтрации является связь между изменяющимся входным сигналом и выходным сигналом, т.е. если входной сигнал является суммой каких-то составляющих, то и выходной сигнал так же будет суммой пропорциональных составляющих (соблюдается принцип суперпозиции). 2. Нелинейную фильтрацию (возведение в степень, извлечение корня, перемножение и т.д.). Здесь выходной сигнал описывается нелинейными дифференциальными уравнениям. На практике обойтись только одной линейной фильтрацией невозможно. Оптимальная согласованная фильтрация. При рассмотрении критерия Котельникова-Зигерта был показан оптимальный приемник, который построен на принципе вычисления корреляционного интеграла, на интервале
где Там отмечалось, что эту задачу можно решить, применяя согласованные фильтры. Однако не существует единого оптимального фильтра, поскольку все зависит от следующих факторов: 1. Какие критерии качества для нас важны, а это определяется назначением радиотехнической системы. Это может быть обнаружение сигнала, отношение сигнал/шум на выходе фильтра, форма сигнала и т.д.. 2. Какие сигналы надо обнаружить (детерминированные, дискретные, непрерывные, случайные). 3. Какие шумы и помехи действуют в радиоканале (флуктуационные, импульсные, сосредоточенные). Итак, смысл оптимальности применим лишь для конкретных моделей сигналов и шумов. Прием дискретных сигналов на согласованный фильтр. Для сигналов с известными параметрами оптимальный фильтр должен дать на выходе максимальный критерий качества, например, максимальное отношение сигнал/шум. Эту операцию можно осуществить за счет свертки сигналов в согласованном фильтре (СФ). Для этого нужно иметь фильтр, импульсная характеристика которого соответствует именно этому сигналу. Известно, что импульсная характеристика согласованного фильтра должна представлять собой сдвинутую на время Импульсная характеристика согласованного фильтра, при
Рис.5.1
Поскольку импульсная характеристика
где В момент Замечательным свойством согласованного фильтра является то, что он обеспечивает наибольшее отношение пикового значения выходного сигнала с среднеквадратическому значению шума, т.е. он обеспечивает максимум правдоподобия ( Здесь обеспечивается именно максимальное отношение сигнал/шум, а не воспроизведение формы сигнала, т.е. все определяется энергией, а не формой сигнала. Рассмотрим некоторые конкретные задачи. Согласованная фильтрация детерминированного сигнала. В этом случае форма обрабатываемого сигнала заранее известна. Характеристики согласованного фильтра здесь полностью определяются известными значениями сигнала. Пусть нам нужно определить лишь факт, что в принятой реализации В формуле (5.2) импульсная характеристику можно представить в виде
где А – постоянный коэффициент. Произведя замену переменных
Если фильтр линейный, то воздействие сигнала и воздействие шума на фильтр можно считать независимыми. Поэтому далее рассмотрим эти два процесса отдельно. Подставляя в (5.2) значение (5.4), получим интеграл свертки сигнала
В выражении (5.5)
где При полной свертке сигнал и его копия полностью совпадают, т.е. сдвига между ними нет (
Таким образом, выходной сигнал Комплексная сопряженность амплитудно-частотной характеристики согласованного фильтра со спектром принимаемого сигнала приводит к компенсации взаимных фазовых сдвигов между спектральными составляющими сигнала в момент
Чем больше Максимальное значение Сочетание компенсации начальных фаз с увеличением амплитуды сильных спектральных составляющих сигнала и обеспечивает оптимальность СФ для обнаружения сигнала на фоне белого шума. Прохождение белого шума через согласованный фильтр. Рассмотрим действие белого шума на согласованный фильтр, импульсная характеристика которого согласована с сигналом. Спектральная плотность шума
где Коэффициент Если спектральная плотность белого шума постоянна, а радиотехническая система ограничена полосой частот
где Подставляя в (5.9) формулу (5.10), получим спектральную плотность шума на выходе согласованного фильтра
Согласно равенству Парсеваля
где С учетом (5.12), формула (5.9) примет вид
Извлекая квадратный корень из (5.13), находим среднеквадратическое значение белого шума
Отношение сигнал/шум на выходе согласованного фильтра. Ранее было показано, что сигнал на выходе согласованного фильтра
а это не что иное, как отношение энергии входного сигнала к спектральной плотности белого шума, которое не зависит от формы сигнала. При рассмотрении методов оптимального когерентного приема в случае неопределенности, подобной в радиолокационных системах, для реализации критерия Неймана-Пирсона используется многоканальный коррелятор. При оптимальной согласованной фильтрации корреляторы каждого канала заменяются согласованными фильтрами (рис. 5.2). В этом случае нет необходимости привязки по времени прихода сигнала.
Рис. 5.2.
Отношение сигнал/шум при небелом шуме. « Белый» шум – это некоррелированный шум. В общем случае шум может быть коррелированным и иметь произвольную спектральную мощность. Для того чтобы «обелить» такой шум, применяют специальный обеляющий фильтр (ОФ) (рис. 5.3),коэффициент передачи которого
Рис. 5.3 Поскольку, обеляющий фильтр внесет свои изменения и в сигнал, то отношение сигнал/шум будет определяться выражением
где
|



 .
. и зеркально перевернутую во времени копию входного сигнала
и зеркально перевернутую во времени копию входного сигнала  (рис.5.1).
(рис.5.1). , равняется нулю, значение
, равняется нулю, значение 
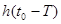 - это тоже самое, что и
- это тоже самое, что и  , то интеграл свертки (интеграл Дюамеля) может быть представлен в виде
, то интеграл свертки (интеграл Дюамеля) может быть представлен в виде ,
,
 - корреляционный сдвиг.
- корреляционный сдвиг. ), а это значит, что
), а это значит, что  .
. ).
). присутствует сигнал. Это критерий качества. Понятно, что согласованный фильтр может не сохранить форму сигнала, т.к. обнаружение требует от согласованного фильтра лишь обеспечить максимальное отношение сигнал/шум. Критерием качества обработки здесь является именно это отношение.
присутствует сигнал. Это критерий качества. Понятно, что согласованный фильтр может не сохранить форму сигнала, т.к. обнаружение требует от согласованного фильтра лишь обеспечить максимальное отношение сигнал/шум. Критерием качества обработки здесь является именно это отношение. ,
,
 .
.
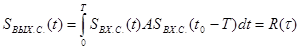 .
.
 ,
,
 .
.
 с точностью до постоянного коэффициента
с точностью до постоянного коэффициента  совпадает с входным сигналом и равен энергии входного сигнала.
совпадает с входным сигналом и равен энергии входного сигнала.
 , тем уже корреляционная функция и тем больше превышение энергии сигнала над уровнем шумов.
, тем уже корреляционная функция и тем больше превышение энергии сигнала над уровнем шумов. на выходе согласованного фильтра определяется только энергией сигнала и не зависит от его формы. При этом коэффициент передачи согласованного фильтра велик на тех частотах, где сосредоточена основная часть энергии полезного сигнала и мал, где спектральная плотность сигнала меньше.
на выходе согласованного фильтра определяется только энергией сигнала и не зависит от его формы. При этом коэффициент передачи согласованного фильтра велик на тех частотах, где сосредоточена основная часть энергии полезного сигнала и мал, где спектральная плотность сигнала меньше. на выходе согласованного фильтра равна произведению спектральной плотности входного шума
на выходе согласованного фильтра равна произведению спектральной плотности входного шума 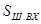 и квадрата модуля коэффициента передачи согласованного фильтра
и квадрата модуля коэффициента передачи согласованного фильтра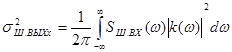 ,
,
 - коэффициент передачи согласованного фильтра.
- коэффициент передачи согласованного фильтра. это амплитудно-частотная характеристика согласованного фильтра, полученная как преобразование Фурье от импульсной характеристики
это амплитудно-частотная характеристика согласованного фильтра, полученная как преобразование Фурье от импульсной характеристики  , то спектральная плотность шума на входе согласованного фильтра
, то спектральная плотность шума на входе согласованного фильтра ,
,
 - спектральная плотность шума.
- спектральная плотность шума. ,
,
 ,
,
 .
. .
.
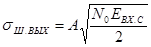 .
.
 . Теперь можно найти отношение сигнал/шум на выходе согласованного фильтра
. Теперь можно найти отношение сигнал/шум на выходе согласованного фильтра
 ,
,


 выбран таким, чтобы компенсировать неравномерность спектра входного небелого шума. На выходе обеляющего фильтра будет получен белый шум со спектральной плотностью N0.
выбран таким, чтобы компенсировать неравномерность спектра входного небелого шума. На выходе обеляющего фильтра будет получен белый шум со спектральной плотностью N0.
 ,
,
 энергия сигнала на выходе ОФ.
энергия сигнала на выходе ОФ.


