Задание 2. Симплекс-метод решения задачи линейного программирования
Сайт: www.melashchuk.com
Решить задачу 1 симплекс-методом. Решение
Приводим задачу к каноническому виду:
Система ограничений задачи является системой уравнений, разрешенной относительно переменных Вычисляем оценки разложений векторов условий по базису опорного решения по формуле:
Опорное решение, коэффициенты разложений и оценки разложений векторов условий по базису опорного решения записываем в симплексную таблицу: 1 2 ↓ 0 0 0
Начальное опорное решение не является оптимальным, так как в рассматриваемой задаче на максимум векторам Х 1, Х 2 соответствуют отрицательные оценки. Найдем новое опорное решение, на котором значение целевой функции будет больше. Так как из всех оценок D i наименьшая оценка Наименьшая из этих оценок
1↓ 2 0 0 0
Опорное решение А 1 не является оптимальным, так как в рассматриваемой задаче на максимум вектору Х 1 соответствует отрицательная оценка. Найдем новое опорное решение. Вводим в базис вектор Х 1. Исключаем из базиса вектор Х 4. За разрешающий элемент принимаем элемент
1 2 0 0 0
Опорное решение Таким образом, Симплекс-метод решения задач линейного программирования (ЗЛП) Симплекс-метод является универсальным методом решения ЗЛП, так как позволяет решить практически любую задачу, представленную в канонической форме. Данный метод состоит в целенаправленном переборе опорных решений ЗЛП. Он позволяет за конечное число шагов расчета либо найти оптимальное решение, либо установить его отсутствие. Алгоритм симплексного метода решения ЗЛП 1. Привести задачу к каноническому виду. Каноническая ЗЛП имеет вид:
Если система ограничений задана в виде неравенств, то для перехода к равенствам достаточно ввести дополнительные переменные. В целевую функцию эти же переменные вводятся с нулевыми коэффициентами.
2. Найти начальное опорное решение с "единичным базисом" (если опорное решение отсутствует, то задача не имеет решения). Опорным решением ЗЛП называется такое допустимое решение Базисом опорного решения называется базис системы векторов условий задачи, включающий в свой состав векторы, соответствующие отличным от нуля координатам опорного решения. 3. Вычислить оценки разложений векторов по базису опорного решения и заполнить таблицу симплексного метода. Оптимальное решение ЗЛП можно найти путем перебора не всех, а только части опорных решений. Для этого необходимо каждое опорное решение проверять на оптимальность и переход от одного опорного решения к другому осуществлять таким образом, чтобы значение целевой функции увеличивалось в задаче на максимум или уменьшалось в задаче на минимум. Для проверки опорного решения на оптимальность необходимо найти оценки разложения вектора условий
где Опорное решение является оптимальным, если: 1) в задаче на максимум все 2) в задаче на минимум все Оптимальное решение ЗЛП является единственным, если для любого вектора условий, не входящего в базис, оценка отлична от нуля, то есть ЗЛП имеет бесконечное множество оптимальных решений, если при оптимальном решении оценка хотя бы одного вектора условия, не входящего в базис, равна нулю, то есть Если хотя бы одна оценка Если опорное решение не является оптимальным, то переходим к следующему опорному решению. Чтобы обеспечить наибольшее изменение целевой функции при переходе от одного опорного решения к другому, векторы, выводимый из базиса и вводимый в базис опорного решения, необходимо выбирать из следующих условий. Вектор, вводимый в базис, из условия: 1) в задаче на максимум 2) в задаче на минимум Вектор, выводимый из базиса, находим из условия:
4. Если выполняется признак единственности оптимального решения, то решение задачи заканчивается. 5. Если выполняется условие существования множества оптимальных решений, то путем простого перебора находят все оптимальные решения.
|




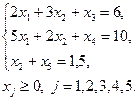
 ,
,  и
и 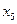 . Свободные (неразрешенные) переменные приравниваем к нулю:
. Свободные (неразрешенные) переменные приравниваем к нулю:  . Получаем
. Получаем  ,
,  ,
,  . Записываем базисное решение
. Записываем базисное решение  , которое является начальным базисным решением с базисом
, которое является начальным базисным решением с базисом 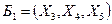 .
. , где
, где  – коэффициенты при базисных переменных в целевой функции;
– коэффициенты при базисных переменных в целевой функции;  – коэффициенты при переменной
– коэффициенты при переменной  в системе ограничений;
в системе ограничений;  – коэффициент при переменной
– коэффициент при переменной 




 , то будем вводить в базис вектор Х 2. Для этого вектора находим оценки
, то будем вводить в базис вектор Х 2. Для этого вектора находим оценки  .
. соответствует вектору Х 5. Поэтому выводим из базиса вектор Х 5. За разрешающий элемент принимаем элемент
соответствует вектору Х 5. Поэтому выводим из базиса вектор Х 5. За разрешающий элемент принимаем элемент  . Получаем опорное решение
. Получаем опорное решение  с базисом
с базисом  :
: . Получаем второе опорное решение
. Получаем второе опорное решение  с базисом
с базисом  :
: является оптимальным, так как для всех векторов условий оценки в задаче на максимум неотрицательные.
является оптимальным, так как для всех векторов условий оценки в задаче на максимум неотрицательные. при
при  .
.

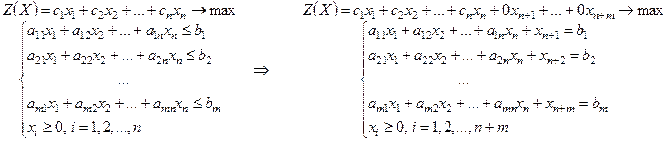
 , для которого векторы условий (столбцы коэффициентов при неизвестных в системе ограничений)
, для которого векторы условий (столбцы коэффициентов при неизвестных в системе ограничений)  , соответствующие положительным координатам, линейно независимы.
, соответствующие положительным координатам, линейно независимы. по базису опорного решения:
по базису опорного решения: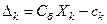 ,
, - вектор коэффициентов целевой функции при базисных переменных;
- вектор коэффициентов целевой функции при базисных переменных; 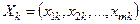 - вектор коэффициентов разложения вектора
- вектор коэффициентов разложения вектора 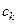 - коэффициент целевой функции при переменной
- коэффициент целевой функции при переменной  .
. ;
; .
. для всех
для всех  .
. .
. в задаче на максимум (
в задаче на максимум ( в задаче на минимум), а при соответствующей переменной нет ни одного положительного коэффициента, то задача не имеет решения из-за неограниченности целевой функции.
в задаче на минимум), а при соответствующей переменной нет ни одного положительного коэффициента, то задача не имеет решения из-за неограниченности целевой функции. ;
; .
. при
при  .
.


