Процесс распространения колебаний в упругой среде называется волной.
В волновом процессе имеет место следующее соотношение:
λ = vT,
где λ – длина волны, Т – период колебаний,
v – скорость распространения волны (фазовая скорость).
Уравнение плоской волны имеет вид:
S = Acos(ωt – r/v)=Acos(wt- kr), где
S– смещение колеблющейся точки от положения равновесия,
A – амплитуда колебаний, ω –циклическая частота колебаний (w = 2π/T),
k= r/v = 2 π/ λ – волновое число,
r – расстояние, пройденное волной от источника колебаний до рассматриваемой точки.
Разность фаз двух колеблющихся точек, находящихся на расстояниях r1 и r2, от источника колебаний, равна:
Δj=j2-j1= -(2 π/ λ)(r1-r2)= -(2 π/ λ)(r1-r2)= -(2 π/ λ) Δ,
где Δ = r1-r2 – разность хода волн.
Примеры решения задач по теме «Механические колебания и волны»
(Номера задач в скобках соответствуют сборнику задач по курсу физики Трофимовой Т.И.)
Задача №1 (4.3). Материальная точка совершает гармонические колебания с амплитудой А = 4 см и периодом Т = 2 с. Напишите уравнение движения точки, если ее движение начинается из положения х0 = 2 см.
| Дано:
A = 4 см =
T = 2 с
t0 = 0
x0 = 2 см =
|
4∙10-2 м
2∙10-2 м
| Решение:
Уравнение гармонических колебаний:
x = A cos(wt+j0).
Связь циклической частоты и периода колебаний:
w = 2π/T= 2π/2=π с-1
|
| x(t) -?
|
| При t0 = 0: x = A cos(j0) а, с другой стороны, x|t = 0= x0. Отсюда x0= A cos(j0).
Тогда φ0 = arccos(x0/A)= arccos(1/2)= π/3.
Подставляя численные значения A, ω и j0, получим требуемое уравнение движения точки: x = 0,04 cos(πt+π/3).
|
| Ответ: x = 0,04 cos(πt+π/3).
|
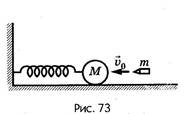
Задача №2 (4.25). На горизонтальной пружине жесткостью k = 900 Н/м укреплен шар массой М = 4 кг, лежащий на гладком столе, по которому он может скользить без трения (рис. 73). Пуля массой m = 10 г, летящая с горизонтальной скоростью v0 = 600 м/с и имеющая в момент удара скорость, направленную вдоль оси пружины, попала в шар и застряла в нем. Пренебрегая массой пружины и сопротивлением воздуха, определите:
1) амплитуду колебаний шара; 2) период колебаний шара.
| Дано:
k = 900 Н/м
M = 4 кг
m= 10 г =
v0 = 600 м/с
|
10-2 кг
| 
|
| A -? T -?
|
|
Решение:
Удар пули о шар является абсолютно неупругим и для него справедлив закон сохранения импульса: P1+P2=P’.
Здесь ось x направлена вдоль оси пружины в сторону полета пули;
P1=mv0 – импульс пули до удара;
P2=0 – импульс шара до удара;
P’=(M+m)u – импульс шара с застрявшей пулей после удара;
u – скорость шара с пулей после удара.
Таким образом, mv0=(M+m)u. Откуда u=mv0/(M+m).
Кинетическая энергия шара с пулей после удара: Ek0=(M+m)u2/2=m2v02/(2(M+m)).
Под действием полученного при ударе импульса пуля с шаром, укрепленным на пружине, совершают колебания. При пренебрежении силами трения эти колебания являются гармоническими колебаниями пружинного маятника, период колебаний которого:
T=2π∙((M+m)/k)1/2=2∙3,14∙((4+0,01)/900)1/2≈6,28∙2/30≈0.419 c.
Из закона сохранения энергии, справедливого для гармонических колебаний:
Ek0=E=Epot.max.
где E – полная механическая энергия маятника;
Epot.max – максимальная потенциальная энергия маятника
(Epot.max= A2k/2, A – амплитуда колебаний).
Отсюда: m2v02/(2(M+m))= A2k/2.
A=mv0/((M+m)k)1/2=10-2∙600/((4+0,01)900)1/2≈6/(2∙30)=0,1 м.
|
| Ответ: A = 0,1 м; T=0,419 c
|
|
|
| Задача №3 (4.28). Однородный диск радиусом R= 20 см колеблется около горизонтальной оси, проходящей на расстоянии l =15 см от центра диска. Определите период T колебаний диска относительно этой оси.
|
|
Дано:
R =20 см =
l = 15 см =
|
0,2 м
0,15 м
|
Решение:
Диск, колеблющийся относительно оси, не проходящей через центр масс, представляет собой физический маятник.
|
| T-?
|
| Период колебаний физического маятника T=2π∙(Jo/(mglc))1/2,
где Jo – момент инерции относительно этой оси;
m – масса диска; lc= l – расстояние от оси до центра масс.
В соответствии с теоремой Штейнера Jo=Jc+ml2,
где Jc – момент инерции относительно центра масс (центра диска).
Так как для диска Jc=mR2/2, то окончательно получим
T=2π∙((mR2/2+ml2)/(mgl))1/2=2π∙(((R2/(2l))+l)/(g))1/2=
=2∙3,14∙((0,22/(2∙0,15)+0,152)/9,81)1/2=1,07 с
|
| Ответ: T=1,07 с
|
| | | | | |
Задача №4 (4.118). Волна распространяется в упругой среде со скоростью v = 150 м/с. Определите частоту ν колебаний, если минимальное расстояние Δx между точками среды, фазы колебаний которых противоположны, равно 0,75 м.
|
Дано:
v =150 м/c
Δx = 0,75 м
|
Решение:
Для бегущей волны фазы колебаний противоположны, если точки среды расположены на расстоянии (2∙n+1)∙λ/2, где n любое целое, λ – длина волны.
|
| ν-?
|
| Отсюда следует, что Δx=λ/2 и λ=2∙ Δx. Длина волны, скорость распространения и частота связаны следующим соотношением: λ= v/ ν.
Отсюда ν= v/ λ= v/(2∙ Δx)=150/(2∙0,75)=100 Гц.
|
| Ответ: ν=100 Гц
|





