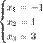СЛУ . Метод гауса
по дисциплине: _________________________
вариант № (тема)
Выполнил ст. гр. _____________ __________________________ (Фамилия И.О.) Проверил: __________________ __________________________ (Фамилия И.О.)
Чита 20__
Примерные вопросы для подготовки к зачету (экзамену) 1. Микроклимат производственных помещений. Параметры микроклимата производственных помещений, их нормирование. Меры профилактики и защиты от неблагоприятного воздействия микроклимата 2. Ионизирующие излучения, их воздействия на организм человека. Защита от действия ионизирующих излучений. 3. Радиоактивность, источники, единицы измерения, способы защиты. 4. Освещение. Виды освещения. Нормирование. Преимущества и недостатки ламп накаливания и газоразрядных ламп. 5. Организация обучения по охране труда. Инструктажи, их виды и методика проведения. 6. Методы и принципы обеспечения безопасности 7. Риск. Виды риска Концепция приемлемого (допустимого) риска 8. Предмет, цели и задачи БЖД. 9. Основные понятия БЖД, определения. 10. Средства обеспечения БЖД 11. Специальная оценка условий труда и декларирование соответствия условий труда нормативным требованиям? 12. Классификация, устройство убежищ и ПРУ 13. Опасные и вредные производственные факторы 14. Химические опасности, токсодоза, ПДК 15. Хлор как АХОВ (характеристика, поражающее действие, источники заражения, способы защиты и оказания помощи). 16. Аммиак как АХОВ (характеристика, поражающее действие, источники заражения, способы защиты и оказания помощи). 17. Химически опасный объект (определение, примеры); аварийно химические опасные вещества, классификация, виды. 18. Химическая авария; зона химического заражения, факторы, определяющие ее масштаб. Правила поведения и меры безопасности. 19. Вибрация, виды, методы защиты 20. Шум, виды шума, методы и средства защиты 21. Инфразвук, ультразвук: характеристика, влияние на человека, средства защиты. 22. Опасность, классификация. Аксиома о потенциальной опасности 23. Ноксосфера и гомосфера 24. Виды освещения. Методы расчета освещения. Контроль производственного освещения 25. Единая государственная система предупреждения и ликвидации чрезвычайных ситуаций, ее основные задачи. 26. Гражданская оборона (определение), задачи в области гражданской обороны. 27. Принципы организации и ведения гражданской обороны, предупреждения и ликвидации чрезвычайных ситуаций. 28. Органы управления, руководство гражданской обороной. 29. Структура РСЧС, ее подсистемы и уровни. 30. Органы управления РСЧС. 31. Силы и средства РСЧС. 32. Режимы функционирования РСЧС, порядок их установления, проводимые мероприятия. 33. Система оповещения о чрезвычайных ситуациях, пункты управления, сигналы оповещения, средства оповещения, порядок доведения до населения. 34. Структура системы гражданской обороны, предупреждения и ликвидации чрезвычайных ситуаций (ГОЧС) объекта (организации). 35. Землетрясение, причины, характеристики, последствия, правила поведения населения. 36. Селевой поток, причины, характеристики, последствия, мероприятия по предупреждению, меры безопасности и правила поведения населения. 37. Наводнение, причины, характеристики, последствия, мероприятия по предупреждению, меры безопасности и правила поведения населения. 38. Оползни, причины, характеристики, последствия, мероприятия по предупреждению, меры безопасности и правила поведения населения. 39. Снежная лавина, причины, характеристики, последствия, мероприятия по предупреждению, меры безопасности и правила поведения населения. 40. Буря (ураган, смерч), причины, характеристики, последствия, меры безопасности и правила поведения населения. 41. Ливни и грозы, причины, характеристики, последствия, меры безопасности и правила поведения населения. 42. Природные опасности, виды и характеристики 43. Биологические опасности 44. Социальные опасности 45. Техногенные опасности, их виды и характеристика 46. Средства коллективной и индивидуальной защиты населения 47. Гражданская оборона 48. Пожар, виды пожаров, горение. 49. Опасные поражающие факторы пожара. Виды горения. Диффузионное и кинетическое горение. 50. Классификация помещений и производств по пожароопасности. Методы и средства тушения пожаров. 51. Взрывы, характеристика поражающих факторов 52. Инфразвук, ультразвук, их источники и средства защиты 53. Электрический ток, его действие на человека 54. Виды тока, пути прохождения через организм человека, первая помощь 55. Виды и вредности производственной пыли 56. ЭМП, характеристика 57. Эргономика, 5 видов совместимости 58. Работоспособность человека и ее динамика. Тяжесть и напряженность труда 59. Охрана труда, принципы, задачи. Управление ОТ. Законодательство об ОТ 60. Что понимается под «выживанием». Основные факторы. 61. Расследование и учет несчастных случаев на производстве.
СЛУ. Метод гауса Система m линейных алгебраических уравнений с n неизвестными (или, линейная система, также употребляется аббревиатура СЛА́У) в линейной алгебре — это система уравнений вида
Система линейных уравнений от трёх переменных определяет наборплоскостей. Точка пересечения является решением. Здесь Система (1) называется однородной, если все её свободные члены равны нулю (b1 = b2 = … = bm = 0), иначе — неоднородной. Система (1) называется квадратной, если число m уравнений равно числу n неизвестных. Решение системы (1) — совокупность n чисел c1, c2, …, cn, таких что подстановка каждого ci вместо xi в систему (1) обращает все её уравнения в тождества. Система (1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если у неё нет ни одного решения. Совместная система вида (1) может иметь одно или более решений. Решения c1(1), c2(1), …, cn(1) и c1(2), c2(2), …, cn(2) совместной системы вида (1) называются различными, если нарушается хотя бы одно из равенств:
Совместная система вида (1) называется определённой, если она имеет единственное решение; если же у неё есть хотя бы два различных решения, то она называется недоопределённой. Если уравнений больше, чем неизвестных, она называется переопределённой. К элементарным преобразованиям системы линейных уравнений относятся: 1)Прибавление к обеим частям одного уравнения соответствующих частей другого, умноженных на одно и то же число, не равное нулю. Принцип метода Гаусса Метод Гаусса включает в себя прямой (приведение расширенной матрицы к ступенчатому виду, то есть получение нулей под главной диагональю) и обратный (получение нулей над главной диагональю расширенной матрицы) ходы. Прямой ход и называется методом Гаусса, обратный - методом Гаусса-Жордана, который отличается от первого только последовательностью исключения переменных. Метод Гаусса идеально подходит для решения систем содержащих больше трех линейных уравнений, для решения систем уравнений, которые не являются квадратными (чего не скажешь про метод Крамера и матричный метод). То есть метод Гаусса - наиболее универсальный метод для нахождения решения любой системы линейных уравнений, он работает в случае, когда система имеет бесконечно много решений или несовместна. Примеры решения систем уравнений Пример Задание. Решить СЛАУ Решение. Выпишем расширенную матрицу системы и при помощи элементарных преобразований над ее строками приведем эту матрицу к ступенчатому виду (прямой ход) и далее выполним обратный ход метода Гаусса (сделаем нули выше главной диагонали). Вначале поменяем первую и вторую строку, чтобы элемент
Далее делаем нули под главной диагональю в первом столбце. Для этого от второй строки отнимаем две первых, от третьей - три первых:
Все элементы третьей строки делим на два (или, что тоже самое, умножаем на
Далее делаем нули во втором столбце под главной диагональю, для удобства вычислений поменяем местами вторую и третью строки, чтобы диагональный элемент равнялся 1:
От третьей строки отнимаем вторую, умноженную на 3:
Умножив третью строку на
Проведем теперь обратный ход метода Гаусса (метод Гассу-Жордана), то есть сделаем нули над главной диагональю. Начнем с элементов третьего столбца. Надо обнулить элемент
Далее обнуляем недиагональные элементы второго столбца, к первой строке прибавляем вторую:
Полученной матрице соответствует система
Ответ.
|

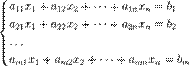
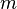 — количество уравнений, а
— количество уравнений, а 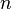 — количество неизвестных. x1, x2, …, xn — неизвестные, которые надо определить. a11, a12, …, amn — коэффициенты системы — и b1, b2, … bm — свободные члены — предполагаются известными[1]. Индексы коэффициентов (aij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно[2].
— количество неизвестных. x1, x2, …, xn — неизвестные, которые надо определить. a11, a12, …, amn — коэффициенты системы — и b1, b2, … bm — свободные члены — предполагаются известными[1]. Индексы коэффициентов (aij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно[2].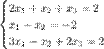 методом Гаусса.
методом Гаусса.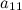 равнялся 1 (это мы делаем для упрощения вычислений):
равнялся 1 (это мы делаем для упрощения вычислений):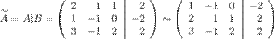
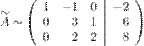
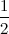 ):
):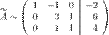
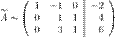

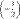 , получаем:
, получаем:
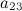 , для этого от второй строки отнимем третью:
, для этого от второй строки отнимем третью:

 или
или