Слоу. Связь решений
Система линейных уравнений является однородной, если свободный член каждого уравнения системы равен нулю. Например: Совершенно ясно, что однородная система всегда совместна, то есть всегда имеет решение. И, прежде всего, в глаза бросается так называемое тривиальное решение Пример 1 Решить однородную систему линейных уравнений Решение: чтобы решить однородную систему необходимо записать матрицу системы и с помощью элементарных преобразований привести её к ступенчатому виду. Обратите внимание, что здесь отпадает необходимость записывать вертикальную черту и нулевой столбец свободных членов – ведь что ни делай с нулями, они так и останутся нулями: (1) Ко второй строке прибавили первую строку, умноженную на –2. К третьей строке прибавили первую строку, умноженную на –3. (2) К третьей строке прибавили вторую строку, умноженную на –1. Делить третью строку на 3 не имеет особого смысла. В результате элементарных преобразований получена эквивалентная однородная система Ответ: Система m линейных однородных уравнений с n переменными имеет ненулевые решения тогда и только тогда, когда определитель матрицы системы равен нулю. Теорема 4.4. Для того, чтобы система однородных уравнений имела ненулевые решения, необходимо и достаточно, чтобы ранг r ее основной матрицы был меньше числа n неизвестных, т. е. r<n. Необходимость. Так как ранг не может превосходить размера матрицы, то, очевидно, r<=n. Пусть r=n. Тогда один из минеров размера nхn отличен от нуля. Поэтому соответствующаясистема линейных уравнений имеет единственное решение:
Значит, других, кроме тривиальных, решений нет. Итак, если есть нетривиальное решение, то r<n. Достаточность: Пусть r<n. Тогда однородная система, будучи совместной, являетсянеопределенной. Значит, она имеет бесчисленное множество решений, т. е. имеет и ненулевые решения. Пусть дана однородная система n линейных уравнений с nнеизвестными
Теорема 4.5. Для того, чтобы однородная система n линейных уравнений с n неизвестными имела ненулевые решения, необходимо и достаточно, чтобы ее определитель был равен нулю, т. е. =0. Если система имеет ненулевые решения, то =0. Ибо при 0 система имеет только единственное, нулевое решение. Если же =0, то ранг r основной матрицы системы меньше числа неизвестных, т.е. r<n. И, значит, система имеет бесконечное множество (ненулевых) решений. Пример 4.6. Решить систему
Положив x3=0,получаем одно частное решение: x1=0, x2=0, x3=0. Положив x3=1, получаем второе частное решение: x1=2, x2=3, x3=1 и т д. Связь решений однородной и неоднородной систем линейных уравнений
Пусть
Системы (25) и (30) в векторной форме имеют вид А×х = в (31) и А×х = 0 (32). По условию А×а = в, А×с = 0. Следовательно, А×(а + с) = А×а + А×с = в + 0 = в. Следовательно, (а + с) – решение уравнения (31), а поэтому и системы (25). 20. Разность двух решений неоднородной системы линейных уравнений есть решение соответствующей однородной системы. Пусть а и с – решения системы (25), а следовательно, и уравнения (31), т.е. А×а = в и А×с = в. Тогда А×(а – с) = А×а – А×с = в – в = 0, т.е. (а – с) – решение уравнения (32), а поэтому и системы (30). 30. Если а – фиксированное частное решение системы (25), а с пробегает все решения системы (30), то (а + с) пробегает все решения системы (25). Согласно 10, при любом с вектор (а + с) будет решением системы (25). Если d – любое решение системы (25), то, согласно 20, разность (d – а) будет решением системы (30). Обозначив (d – а) = с, получим d = (а + с). Теорема 29. Если а – частное решение линейной неоднородной системы уравнений и а1, а2, …, аn–r – фундаментальная система решений соответствующей однородной системы уравнений, то общее решение данной неоднородной системы имеет вид d = а + С1а1 + С2а2 + … + Сn–r аn–r, где С1, С2, …, Сn–r – любые элементы поля Р. (Иными словами, общее решение системы линейных неоднородных уравнений равно сумме частного решения этой системы и общего решения соответствующей однородной системы.) Доказательство является следствием предыдущих свойств.
|




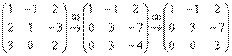
 , и, применяя обратный ход метода Гаусса, легко убедиться, что решение единственно.
, и, применяя обратный ход метода Гаусса, легко убедиться, что решение единственно.

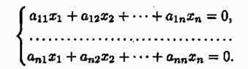


 (25) произвольная система линейных неоднородных уравнений с коэффициентами из поля Р. Если в этой системе все свободные члены заменить нулями, то полученная система линейных однородных уравнений называется соответствующей однородной системой (это система (30)). Решения систем (25) и (30) удовлетворяют следующим свойствам:
(25) произвольная система линейных неоднородных уравнений с коэффициентами из поля Р. Если в этой системе все свободные члены заменить нулями, то полученная система линейных однородных уравнений называется соответствующей однородной системой (это система (30)). Решения систем (25) и (30) удовлетворяют следующим свойствам: (30)
(30)



