Устойчивость дискретных системПри отсутствии входного сигнала в дискретной системе могут существовать свободные колебания. Их вид зависит от начальных условий, то есть значений, хранящихся в элементах памяти системы в момент отключения входного сигнала. Система называется устойчивой, если при любых начальных условиях свободные колебания являются затухающими, то есть если при x(k) - 0
Любой сигнал на выходе линейной стационарной системы представляет собой линейную комбинацию ее задержанных во времени импульсных характеристик. Поэтому для затухания свободных колебаний необходимо, чтобы была затухающей импульсная характеристика системы h(k):
В предыдущем разделе было показано, что импульсная характеристика системы в общем случае содержит слагаемые вида
гае Такие слагаемые при
Теперь мы можем окончательно сформулировать условие устойчивости: чтобы дискретная система была устойчива, полюсы ее функции передачи должны находиться па комплексной плоскости внутри круга единичного радиуса.
|
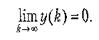
— полюсы функции передачи системы, п — неотрицательные целые числа, меньшие кратности полюса 
затухают, если полюс 
