Сущность линейной дискретной обработки
Вообще, дискретный фильтр — это произвольная система обработки дискретного сигнала, обладающая свойствами линейности и стационарности. Под этими свойствами понимается то же, что и в аналоговом случае: линейность означает, что выходная реакция на сумму сигналов равна сумме реакций на эти сигналы, поданные на вход по отдельности, а стационарность — что задержка входного сигнала приводит лишь к такой же задержке выходного сигнала, не меняя его формы. ЗАМЕЧАНИЕ ---------------------------------------------------------------------------- Существуют и фильтры с переменными параметрами, не обладающие свойством стационарности. Это, например, адаптивные фильтры, меняющие свои параметры в зависимости от статистических свойств входного сигнала. Любой фильтр обладает определенной частотной характеристикой. Чтобы она была нетривиальной, то есть чтобы коэффициент передачи фильтра на разных частотах был разным, выходной сигнал фильтра y(k) должен зависеть от нескольких отсчетов входного сигнала x(k). Таким образом, дискретный фильтр должен обладать памятью. Чтобы обеспечить линейность и стационарность, производимые фильтром математические операции должны ограничиваться сложением и умножением на константы. Рассмотрим простейший пример. Пусть выходной сигнал фильтра равен сумме двух последних отсчетов входного сигнала:
Убедимся в том, что эта система по-разному пропускает на выход сигналы разных частот: подадим на вход фильтра серию одинаковых отсчетов (то есть сигнал нулевой частоты):
Как видите, уровень постоянного сигнала фильтр увеличил в два раза. Теперь подадим на вход отсчеты, одинаковые по модулю, но с чередующимися знаками (то есть отсчеты гармонического сигнала с частотой Найквиста):
В отличие от постоянного сигнала, сигнал с частотой Найквиста на выход просто не прошел. Далее попробуем что-нибудь промежуточное, например сигнал с частотой, равной половине частоты Найквиста:
На выходе в данном случае получаются отсчеты синусоиды, имеющей в -Jl раз большую амплитуду и некоторый фазовый сдвиг по сравнению со входным сигналом. Рассмотренный пример представляет собой простейший случай нерекурсивного фильтра. Такие фильтры суммируют некоторое число входных отсчетов, умножая их при этом на постоянные весовые коэффициенты. Теперь заметим, что помимо выходных отсчетов мы можем использовать для вычислений и ранее рассчитанные значения выходного сигнала. Попробуем просто суммировать входной отсчет и предыдущий выходной отсчет:
Подаем на вход постоянный сигнал (начальное состояние фильтра считаем нулевым):
Так, очевидно, будет продолжаться и далее — выходной сигнал будет линейно нарастать, что рано или поздно приведет к переполнению разрядной сетки вычислительного устройства. Это сразу же демонстрирует нам главную отличительную черту фильтров, использующих при вычислениях предыдущие отсчеты выходного сигнала (их называют рекурсивными фильтрами) — из-за наличия обратных связей они могут быть неустойчивыми. Попробуем уменьшить влияние обратной связи, разделив предыдущий отсчет выходного сигнала на 2:
Снова подаем па вход постоянный сигнал:
Как видим, ситуация радикально изменилась — теперь выходной сигнал с уменьшающейся скоростью стремится к значению 2. Таким образом, переходный процесс в фильтре является бесконечным. Это еще одна отличительная черта рекурсивных фильтров. Итак, рекурсивные фильтры суммируют при расчетах не только входные, но и некоторое количество предыдущих выходных отсчетов сигнала, умножая их при этом на постоянные весовые коэффициенты. В общем случае дискретный фильтр суммирует (с весовыми коэффициентами) некоторое количество входных отсчетов (включая последний) и некоторое количество предыдущих выходных отсчетов:
где Данная формула называется алгоритмом дискретной фильтрации. Если по-иному сгруппировать слагаемые, чтобы с одной стороны от знака равенства были только входные отсчеты, а с другой — только выходные, получим форму записи, называемую разностным уравнением:
Структура разностного уравнения похожа на структуру дифференциального уравнения аналоговой линейной системы, только вместо операции дифференцирования в формуле фигурируют задержки дискретных последовательностей. Как мы увидим далее, этим определяется и общность подходов к описанию аналоговых и дискретных систем. Однако весьма существенным является то, что в дискретной системе не существует каких-либо принципиальных ограничений на соотношение между т и п — количествами входных и выходных отсчетов, используемых при вычислениях. Дискретные системы, как и аналоговые, могут описываться различными способами. Благодаря сходству свойств z-преобразования со свойствами преобразований Лапласа и Фурье способы описания аналоговых и дискретных систем в основном похожи друг на друга. Кроме того, практически каждый способ описания дискретной системы соответствует определенной структурной схеме.
|

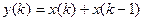










 и
и 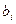 - вещественные коэффициенты.
- вещественные коэффициенты.