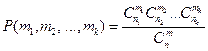Элементы комбинаторики. Теорема. Пусть даны m групп элементов, причем i-я группа состоит из ni элементов

Теорема. Пусть даны m групп элементов, причем i -я группа состоит из n_i элементов. Общее число N способов, с помощью которых можно осуществить указанный выбор, определяется равенством

Это выражение называют основной формулой комбинаторики.

Определение. Результат выбора m элементов из группы, содержащей n элементов, будем называть выборкой из n элементов по m. Если при этом элемент после выбора снова возвращается в группу, то выборку называют выборкой с возвращением. Бели же выбранный элемент не участвует в дальнейшем выборе, то выборку называют выборкой без возвращения.

Заметим, что в любом случае результат выбора m элементов из группы, содержащей n элементов, будем называть выборкой.

Определение. Выборку, в которой не учитывают порядок выбора элементов, называют сочетанием, а выборку, в которой учитывают порядок выбора элементов, − размещением. При этом если рассматривают выборку с возвращением, то сочетание (размещение) называют сочетанием (размещением) с повторениями, а если рассматривают выборку без возвращения, то сочетание (размещение) называют сочетанием (размещением) без повторений, или просто сочетанием (размещением).

Замечание. Размещение без повторений из n элементов по n элементов называют перестановкой из n элементов.

Теорема. Число размещений (без повторений) из n элементов по m определяется формулой

Теорема. Число сочетаний (без повторений) из n элементов по m определяется формулой

Теорема. Число размещений с повторениями из n элементов по m определяется формулой .

Теорема. Число сочетаний с повторениями из n элементов по m определяется формулой

Рассмотрим еще одну часто встречающуюся на практике задачу комбинаторики. Требуется найти число размещений с повторениями из n элементов по m элементов, в которых первый элемент встречается ровно m 1 раз, второй элемент встречается ровно m 2 раз,..., n -й элемент встречается ровно mn раз (m 1 + m 2 +... + mn = m). Число таких размещений обозначим С (m 1, m 2,..., mn). Теорема. Число С (m 1, m 2,..., mn) определяется формулой

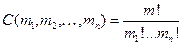
Гипергеометрическая схема Пусть имеется n = n 1 +... + nk различных элементов, причем из них n 1 элементов первого типа, n 2 − второго типа,..., nk − nk -го типа. Случайным образом из этих элементов выбираются m элементов. Вероятность события А, состоящего в том, что среди выбранных элементов окажется ровно m 1 ≤ n 1 элементов первого типа, m 2 ≤ n 2 второго типа,..., mk ≤ nk элементов nk -го типа, m 1 + m 2 +... + mk = m, обозначают P (m 1, m 2,..., mk). Определение. Рассмотренный способ выбора элементов называют гипергеометрической схемой, а совокупность вероятностей P (m 1, m 2,..., mn) в гипергеометрической схеме при фиксированных n, m, ni, , и различных mi, , m 1 + m 2 +... + mn = m, называют гипергеометрическим распределением. Теорема. Вероятности P (m 1, m 2,..., mk) в гипергеометрической схеме определяют по формуле