Свойства операций над событиями
1. Коммутативность суммы и произведения: 2. Ассоциативность суммы и произведения:
3. Дистрибутивность относительно сложения: 4. Дистрибутивность относительно умножения (новое свойство, не выполняющееся для чисел): 5. Включение А в В, т.е. 6. Совпадение двойного дополнения с исходным событием: 7. Совпадение суммы и произведения одинаковых событий с самим событием 8. Законы де Моргана: Определение. Сигма-алгеброй (σ-алгеброй) называют непустую систему подмножеств некоторого множества B, удовлетворяющую следующим двум условиям. 1. Если подмножество А принадлежит B, то дополнение A принадлежит B. 2. Если подмножества A 1, A 2,..., An,... принадлежат B, то их объединение и их пересечение принадлежит B. Рассмотрим пространство элементарных исходов Ω. Элементы некоторой σ-алгебры B, заданной на Ω, будем называть событиями. В этом случае σ-алгебру B принято называть сигма-алгеброй (σ-алгеброй) событий. Любая σ-алгебра событий содержит достоверное событие Ω и невозможное событие В случае конечного или счетного пространства элементарных исходов Ω в качестве σ-алгебры событий обычно рассматривают множество всех подмножеств Ω. Замечание. Если в условии 2 счетное множество событий заменить на конечное, то получим определение алгебры событий. Любая σ-алгебра событий обязательно является алгеброй событий. Обратное утверждение, вообще говоря, не верно.
|

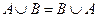 ,
,  .
. , (АВ) С = А (ВС).
, (АВ) С = А (ВС).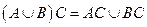 .
. .
. , влечет за собой включение
, влечет за собой включение  в
в 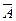 , т.е.
, т.е.  .
.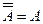 .
.

 .
.


