Схема Бернулли
Повторные испытания – это последовательное проведение n раз одного и того же опыта или одновременное проведение n одинаковых опытов. Например, при контроле уровня надежности прибора могут либо проводить n испытаний с одним и тем же прибором, если после отказа полностью восстанавливают его исходные свойства, либо ставить на испытания n опытных образцов этого прибора, которые считают идентичными. Определение. Схемой Бернулли (или последовательностью независимых одинаковых испытаний, или биномиальной схемой испытаний) называют последовательность испытаний, удовлетворяющую следующим условиям: 1) при каждом испытании различают лишь два исхода: появление некоторого события A, называемого „успехом", либо появление его дополнения 2) испытания являются независимыми, т.е. вероятность успеха в k -м испытании не зависит от исходов всех испытаний до k -гo; 3) вероятность успеха во всех испытаниях постоянна и равна
Вероятность неудачи в каждом испытании обозначим q, т.е.
Пример. Последовательное подбрасывание n раз симметричной монеты (здесь успехом является появление „герба" с вероятностью р = 1/2) или последовательное бросание n раз игральной кости (здесь успехом можно считать, например, появление шестерки с вероятностью р = 1/6). Эти две реальные схемы испытаний являются примером идеального соответствия схеме испытаний Бернулли. Теорема. Вероятность P n (k) того, что в n испытаниях по схеме Бернулли произойдет ровно к успехов, определяется формулой Бернулли
Следствие. Вероятность появления успеха (события А) в n испытаниях не более k 1 раз и не менее k 2 раз равна:
Следствие. В частном случае при k 1 = 1 и k 2 = n получаем формулу для вычисления вероятности хотя бы одного успеха в n испытаниях: При больших значениях числа испытаний n использование формулы Бернулли затруднительно в вычислительном плане. Здесь существенную помощь могут оказать приближенные формулы. Пусть число испытаний n по схеме Бернулли „велико", а вероятность успеха р в одном испытании „мала", причем „мало" также произведение
называемой формулой Пуассона. Совокупность вероятностей Если в схеме Бернулли число испытаний n „велико", причем „велики" также вероятности р успеха и q неудачи, то для всех к справедлива приближенная формула
называемая локальной формулой Муавра – Лапласа, где
Функцию Если число n испытаний по схеме Бернулли „велико", причем „велики" также вероятности р успеха и q неудачи, то для вероятности
где
Функцию Ф(х) называют функцией стандартного нормального (или гауссова) распределения. Определение. Функцию
называют интегралом Лапласа. Используя интеграл Лапласа, интегральную формулу Муавра – Лапласа можно записать в виде
Значения функций
|

 , называемого „неудачей";
, называемого „неудачей"; .
.

 , если в n испытаниях успех „У" имел место i раз, а неуспех „Н", следовательно, n – i раз.
Событие Ak происходит всякий раз, когда реализуется элементарный исход ω, в котором i = k. Вероятность любого такого элементарного исхода равна
, если в n испытаниях успех „У" имел место i раз, а неуспех „Н", следовательно, n – i раз.
Событие Ak происходит всякий раз, когда реализуется элементарный исход ω, в котором i = k. Вероятность любого такого элементарного исхода равна  .
Число таких исходов совпадает с числом способов, которыми можно расставить k букв „У" на n местах, не учитывая порядок, в котором их расставляют. Число таких способов равно
.
Число таких исходов совпадает с числом способов, которыми можно расставить k букв „У" на n местах, не учитывая порядок, в котором их расставляют. Число таких способов равно  .
Так как Ak есть объединение (сумма) всех указанных элементарных исходов, то окончательно получаем искомую формулу для вероятности.
.
Так как Ak есть объединение (сумма) всех указанных элементарных исходов, то окончательно получаем искомую формулу для вероятности.
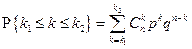
 .
. . Тогда Рn (k) определяют по приближенной формуле
. Тогда Рn (k) определяют по приближенной формуле
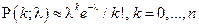 называют распределением Пуассона. Формула Пуассона справедлива также для числа неудач, но только в том случае, когда „мало"
называют распределением Пуассона. Формула Пуассона справедлива также для числа неудач, но только в том случае, когда „мало"  .
.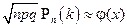
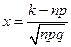 ,
, 
 называют плотностью стандартного нормального (или гауссова) распределения.
называют плотностью стандартного нормального (или гауссова) распределения. того, что число успехов к заключено в пределах от k 1 до k 2, справедливо приближенное соотношение называемое интегральной формулой Муавра – Лапласа,
того, что число успехов к заключено в пределах от k 1 до k 2, справедливо приближенное соотношение называемое интегральной формулой Муавра – Лапласа,
 ,
,  ,
, 


 ,
, 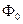 приведены в таблицах.
приведены в таблицах.


