Типовые механические среды
Характер движения зависит не от величины сил, а от той среды, к которой приложены силы. Среда характеризуется способностью создавать противосилы. В механике имеются три типовые среды, с которыми в большинстве случаев и взаимодействует источник силы. От этого взаимодействия получаются перечисленные выше характеры движения. Соответственно имеются следущие типовые механические среды: · упругая; · инерционная; · вязкая.
Типичным примером является пружина, рис. 5.При взаимодействии источника силы с пружиной она мгновенно сжимается, с тем чтобы ответить противосилой, источник силы делает скачок на величину s. Величина скачка зависит от жесткости пружины С. Чем больше жесткость, тем меньше величина перемещения. С этой целью и делают, например, жесткий пол, чтобы он не продавливался при ходьбе человека по полу. В этом случае источником силы является человек, которого притягивает Земля с величиной его веса. Эта сила не изменяется при перемещении человека, а половицы являются той средой, с которой взаимодействует человек. Они прогибаются, чтобы создать противосилу. Конечно, пружина — это образ упругой среды. К таким средам относятся резина, упругий мяч, поршень цилиндра, сжимающего воздух, и многое тому подобное другое. Инерционная среда. Это среда, которая создает противосилы, пропорциональные ускорению с обратным знаком. Типичным примером является тело, имеющее массу. Коэффициент пропорциональности в этом случае также называют массой. Это послужило тому, что иногда массу называют мерой инертности тела, что, впрочем, в нашем курсе делать не будем, потому что, как правило, масса в механизмах прямо не исчисляется, а имеют дело с так называемой приведенной к данному перемещению массой. Это подробно рассматривается, например, при изучении регуляторов частоты вращения дизель-генераторов.
Вязкая среда. Это среда, которая создает противосилы, пропорциональные скорости с обратным знаком. Типичным представителем этой среды являются различного рода жидкости, воздух и другие тому подобные среды.
Рис. 7. Образ вязкой среды
Вязкая среда отличается от двух выше указанных сред тем, что никогда не отдает работу, которую затратил источник силы. Действительно, сжатая пружина разжимается, масса останавливается, отдавая работу, но вязкая среда никогда работу не отдает, куда бы ни было направлено движение тела. Уяснить это можно, рассмотрев приращение работы вязкой среды: dA= - Квт• (ds/dt)•ds= - Квт• (ds2/dt). Но ds2 всегда положительная величина. Поэтому в целом величина dA всегда отрицательна. Силы вязкого трения, всегда поглощающие работу, называют еще диссипативными силами (рассеивающими работу). Они необходимы для поглощения всякого рода колебаний. Организация вязких сред в механизмах и агрегатах подчас является необходимым условием устойчивой работы механизма. Хотя, конечно, силы вязкого трения уменьшают коэффициент полезного действия механизма. В заключение заметим (изменив местами инерционную и вязкую среды), что природа создала стройную систему сред: · упругую Fу= - С•s; · вязкую Fв= - Квт• (ds/dt); · инерционную Fи= - M•(d2s/dt2), — которые отличаются друг от друга только степенью производной от перемещения (и, конечно, названием коэффициентов пропорциональности, что принципиально не существенно). Рассмотрим задачу. Надо определить параметры движения т/х «Ладога». Водоизмещение — 2925 т, скорость — 12 узлов, мощность главных двигателей — 1280 кВт, 1280х4/3=1707 л.с. (для практических расчетов и с учетом принципа идеализации КПД винта принимаем равным 1). Масса — 2925000 кг, скорость хода номинальная — 12х1852/3600=6,17 м/с, мощность номинальная — 1280000 Вт. Сила FN на упорных подшипниках 1280000/6,17=207455,4. Н=~ 20745 кгс~=21т Коэффициент вязкого трения FN / VN=207455/6,17=33623 Нс/м. Сумма всех сил всегда должна быть равна нулю.
Прежде чем подставить численные значения, рассмотрим упрощающие преобразования, приводящие уравнение к некоторому стандартному виду. Все преобразования делаются на основе тождественных преобразований, а именно: деление и умножение на одно и то же число, сложение и вычитание одного и того же числа, деление или умножение обеих частей уравнения на одно и то же число. Такие преобразования не изменяют исходного физического уравнения. Перейдем к относительным единицам, разделив обе части уравнения на FN:
Обычно относительные значения обозначают, как правило, малыми соответствующими буквами. Так:
Приходим к следующему простому уравнению:
или с учетом перехода к относительному времени
Его решение, при номинальной силе
Удобно перейти к так называемой постоянной удвоения Т2 = Та*0,67≈ Та*0,7. С ее помощью легко на практике строить процесс разгона или торможения судна, для чего по оси времени откладывают отрезки времени Т2, а по оси ординат — половины разности между установившимся значением переменной и точкой, полученной на предыдущем шаге построения функции.
Так, построение функции разгона судна, если дали полный вперед (f =1), будет выглядеть так, как показано на рис. 8.
Рис. 8. Построение графика разгона судна Как видим, уже после четырех-пяти промежутков Т2, то есть около 4 — 5 минут (для судов типа «ЛАДОГА»), судно достигнет установившейся скорости движения. Уравнение судна при остановке главных двигателей:
Физически в этом случае имеем силу вязкого трения, которая уравновешивается силой инерции. С уменьшением скорости и сила инерции должна уменьшаться, то есть должно уменьшаться ускорение, что и будет происходить вплоть до скорости и ускорения, равных нулю. Непосредственной подстановкой определяем, что
Рис. 9. Построение графика остановки судна
Интересной информацией, полученной из этого уравнения, является путь, который пройдет судно после остановки главных двигателей:
Это значит, что судно пройдет путь, численно равный единице скорости, измеренной в относительных единицах времени (с базовым значением времени Та), то есть за время Та. В последней колонке приведенной выше таблицы дано значение этой скорости, численно равной искомому пути. Так, для теплохода типа «Ладога 289» этот путь будет равен 6,17*87̊≈537 м. Как видим, этот путь немалый, от половины до километра. Поэтому при швартовке реверс движителей необходим для торможения судна.
|




 =0 откуда
=0 откуда 
 .
. ,
,  .
.
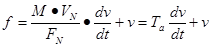
 имеем
имеем .
. , будет
, будет  . Это проверяется непосредственной подстановкой решения в уравнение.
. Это проверяется непосредственной подстановкой решения в уравнение.


 или
или  .
.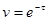 .
.
 .
.


