Примеры непрерывные случайных величин
Равномерное распределение. Случайная величина имеет равномерное распределение на отрезке [ а, b ], если ее плотность распределения
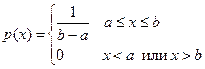 ,
, 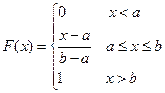
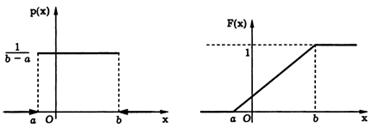
Вероятность попадания равномерно распределенной случайной величины в интервал (х 1, x 2), лежащий внутри отрезка [ a, b ], равна F (x 2) − F (x 1) = (x 2 − x 1)/(b − а), т.е. пропорциональна длине этого интервала. Таким образом, равномерное распределение реализует схему геометрической вероятности при бросании точки на отрезок [ a, b ].
Экспоненциальное распределение. Случайная величина распределена по экспоненциальному (показательному) закону, если она имеет плотность распределения
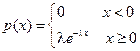 ,
, 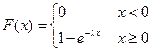
где λ > 0 − параметр экспоненциального распределения.
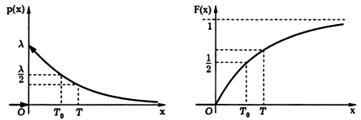
Экспоненциально распределенная случайная величина может принимать только положительные значения. Примером случайной величины, имеющей экспоненциальное распределение, является время распада радиоактивных элементов.
Экспоненциально распределенная случайная величина X обладает весьма важным свойством, которое естественно назвать отсутствием последействия. Трактуя X как время распада атома, рассмотрим событие
A = { xi < X < х 1 + x 2}
и найдем условную вероятность этого события при условии выполнения события В = { X > х 1}. В соответствии с определением условной вероятности P(A | B) = P(AB)/P(B). Но событие AB,как нетрудно понять, совпадает с событием А. Поэтому P(A | B) = P(A)/P(B). Далее, используя свойство 4 функции распределения, имеем: 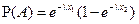 , , 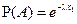 . Значит, . Значит, 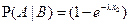 , то есть вероятность распада атома за время х 2 при условии, что перед этим он уже прожил время х 1, совпадает с безусловной вероятностью распада того же самого атома за время x 2. Именно это свойство и представляет собой отсутствие последействия. Допуская некоторую вольность речи, отсутствие последействия можно трактовать как независимость остаточного времени жизни атома от того времени, которое он уже прожил. Можно показать и обратное: если случайная величина X обладает свойством отсутствия последействия, то она обязательно должна быть распределена по экспоненциальному закону. Таким образом, отсутствие последействия является характеристическим свойством экспоненциально распределенных случайных величин. , то есть вероятность распада атома за время х 2 при условии, что перед этим он уже прожил время х 1, совпадает с безусловной вероятностью распада того же самого атома за время x 2. Именно это свойство и представляет собой отсутствие последействия. Допуская некоторую вольность речи, отсутствие последействия можно трактовать как независимость остаточного времени жизни атома от того времени, которое он уже прожил. Можно показать и обратное: если случайная величина X обладает свойством отсутствия последействия, то она обязательно должна быть распределена по экспоненциальному закону. Таким образом, отсутствие последействия является характеристическим свойством экспоненциально распределенных случайных величин.
|
Нормальное распределение. Случайная величина распределена по нормальному (или гауссову) закону, или имеет нормальное (гауссово) распределение, если ее плотность
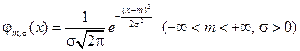
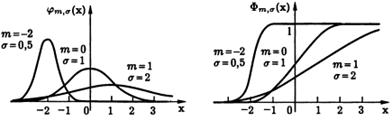
Нормальное распределение зависит от двух параметров: m, называемого математическим ожиданием или средним значением, и σ, называемого средним квадратичным отклонением.
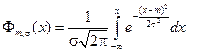
Если m = 0 и σ = 1, то такой нормальный закон называют стандартным и его функцию распределения обозначают Ф(x), а плотность распределения − φ(х). С плотностью и функцией стандартного нормального распределения мы уже встречались в локальной и интегральной формулах Муавра−Лапласа.
Гамма-распределение. Другим распределением, также достаточно хорошо описывающим времена безотказной работы различных технических устройств, является гамма-распределение с плотностью
 , , 
 − гамма-функция Эйлера, обладающая следующими полезными свойствами: − гамма-функция Эйлера, обладающая следующими полезными свойствами:  и и  . .

|

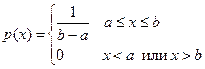 ,
, 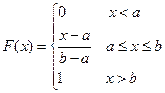

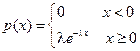 ,
, 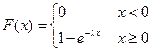

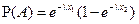 ,
, 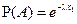 . Значит,
. Значит, 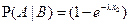 , то есть вероятность распада атома за время х 2 при условии, что перед этим он уже прожил время х 1, совпадает с безусловной вероятностью распада того же самого атома за время x 2. Именно это свойство и представляет собой отсутствие последействия. Допуская некоторую вольность речи, отсутствие последействия можно трактовать как независимость остаточного времени жизни атома от того времени, которое он уже прожил. Можно показать и обратное: если случайная величина X обладает свойством отсутствия последействия, то она обязательно должна быть распределена по экспоненциальному закону. Таким образом, отсутствие последействия является характеристическим свойством экспоненциально распределенных случайных величин.
, то есть вероятность распада атома за время х 2 при условии, что перед этим он уже прожил время х 1, совпадает с безусловной вероятностью распада того же самого атома за время x 2. Именно это свойство и представляет собой отсутствие последействия. Допуская некоторую вольность речи, отсутствие последействия можно трактовать как независимость остаточного времени жизни атома от того времени, которое он уже прожил. Можно показать и обратное: если случайная величина X обладает свойством отсутствия последействия, то она обязательно должна быть распределена по экспоненциальному закону. Таким образом, отсутствие последействия является характеристическим свойством экспоненциально распределенных случайных величин.
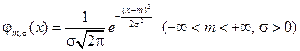
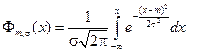

 ,
, 
 − гамма-функция Эйлера, обладающая следующими полезными свойствами:
− гамма-функция Эйлера, обладающая следующими полезными свойствами:  и
и  .
.




