Определение. Математическим ожиданием (средним значением) MX непрерывной случайной величины называют интеграл
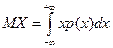
При этом предполагается, что

Дисперсия вычисляется по формуле 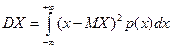
Пример 4. Математическое ожидание и дисперсия равномерно распределенной на отрезке [ а, b ] случайной величины X
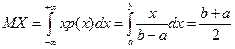 ,
, 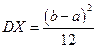
Пример 5. Математическое ожидание и дисперсия случайной величины X, распределенной по нормальному закону с параметрами m и σ:
 ,
, 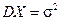
Пример 6. Математическое ожидание и дисперсия случайной величины X, имеющей экспоненциальное распределение
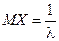 ,
, 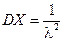
Пример 7. Математическое ожидание и дисперсия случайной величины X, имеющей гамма-распределение
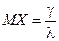 , ,  Модой случайной величины X непрерывного типа называется действительное число dx, определяемое как точка максимума плотности распределения вероятностей fX (х).
Медианой случайной величины X непрерывного типа называется действительное число hx, удовлетворяющее условию
P{ X < hx } = P{ X ≥ hx },
т.е. корень уравнения FX (x) = 1/2. Так как данное уравнение может иметь множество корней, то медиана определяется, вообще говоря, неоднозначно.
Квантилью порядка р (симметричной квантилью порядка р)распределения случайной величины X непрерывного типа называется действительное число tp (действительное число
Модой случайной величины X непрерывного типа называется действительное число dx, определяемое как точка максимума плотности распределения вероятностей fX (х).
Медианой случайной величины X непрерывного типа называется действительное число hx, удовлетворяющее условию
P{ X < hx } = P{ X ≥ hx },
т.е. корень уравнения FX (x) = 1/2. Так как данное уравнение может иметь множество корней, то медиана определяется, вообще говоря, неоднозначно.
Квантилью порядка р (симметричной квантилью порядка р)распределения случайной величины X непрерывного типа называется действительное число tp (действительное число 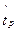 ), удовлетворяющее уравнению ), удовлетворяющее уравнению
 ( (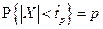 ) )
|

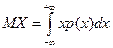

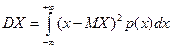
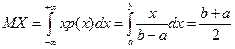 ,
, 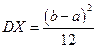
 ,
, 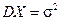
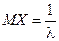 ,
, 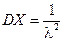
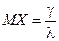 ,
,  Модой случайной величины X непрерывного типа называется действительное число dx, определяемое как точка максимума плотности распределения вероятностей fX (х).
Медианой случайной величины X непрерывного типа называется действительное число hx, удовлетворяющее условию
P{ X < hx } = P{ X ≥ hx },
т.е. корень уравнения FX (x) = 1/2. Так как данное уравнение может иметь множество корней, то медиана определяется, вообще говоря, неоднозначно.
Квантилью порядка р (симметричной квантилью порядка р)распределения случайной величины X непрерывного типа называется действительное число tp (действительное число
Модой случайной величины X непрерывного типа называется действительное число dx, определяемое как точка максимума плотности распределения вероятностей fX (х).
Медианой случайной величины X непрерывного типа называется действительное число hx, удовлетворяющее условию
P{ X < hx } = P{ X ≥ hx },
т.е. корень уравнения FX (x) = 1/2. Так как данное уравнение может иметь множество корней, то медиана определяется, вообще говоря, неоднозначно.
Квантилью порядка р (симметричной квантилью порядка р)распределения случайной величины X непрерывного типа называется действительное число tp (действительное число 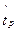 ), удовлетворяющее уравнению
), удовлетворяющее уравнению
 (
(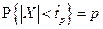 )
)



