Геометрическая сторона задачи
Анализируя деформацию элемента на поверхности вала видим, что элемент по граням смещается, т.е. подвергается сдвигу. Элемент, находящийся только под действием касательных напряжений подвергается чистому сдвигу и называется площадкой чистого сдвига (П.Ч.С.) (рисунок 1.5).
Таким образом, при кручении каждая точка вала находится в напряженном состоянии чистого сдвига. Решая обратную задачу видим, что для площадки чистого сдвига главные площадки повернуты на 45º, а главные напряжения равны по величине касательному напряжению (рисунок 1.6).
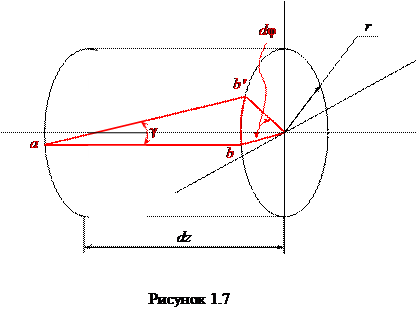
Выделим из вала бесконечно малый элемент длины dz (рисунок 1.7). Проведем анализ угла сдвига γ. Учитывая, что угол небольшой, то tg φ ≈ φ.
где θ – погонный или относительный угол закручивания.
Аналогично для произвольной точки вала получим зависимость
|






 .
.