Физическая сторона задачиПолучим закон Гука при кручении по аналогии с растяжением-сжатием.
где G – модуль упругости второго рода (модуль сдвига), например Gсталь = 8∙104 МПа.
Синтез Решая совместно (14.1), (14.4), (14.5) получим формулу для касательных напряжений произвольной точки вала при кручении
Максимальные напряжения возникают на поверхности вала, т.е. при максимальном радиусе (при ρ = ρmax = r = d/2).
где Таким образом, при кручении максимальное напряжение возникает на поверхности вала, а минимальное ближе к его центру, т.е. эпюра касательных напряжений имеет следующий вид (рисунок 1.8).
Таким образом при кручении наиболее рациональными являются пустотелые валы или валы кольцевого сечения. Рассматривая четыре стороны задачи с точки зрения деформаций можно получить зависимость для угла закручивания вала
где
|
– полярный момент сопротивления, характеризует способность вала заданного диаметра выдерживать соответствующий крутящий момент, измеряется в [м3].
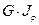– жесткость сечения вала;
– жесткость вала.
