Дәріс. Шектелген спектрі бар сигналдар және олардың математикалық моделдері. Котельников теоремасы
дәріс. Шектелген спектрі бар сигналдар және олардың математикалық моделдері. Котельников теоремасы. Өзінің спектрі бойынша сигналды қайта қалпына келтіру үшін нөлден шексіздікке дейінгі аралықта жатқан жиіліктері бар құрастырушылардың барлығын ескеру қажет. Бірақ бұл процедура физикалық көзқарас жағынан тіпті мүмкін емес. Сонымен қатар спектралдық құрастырушылардың w®¥ -дағы үлесі сигналдардың энергиясының шектелгендігінен тіптен де кішкентай. Және де сигналдарды таратуға және өңдеуге арналған қандай да болмасын іс жүзіндегі құрылғының өткізу жолағының шекті ені бар. Сондықтан, сигналдың мынандай қасиеті бар математикалық моделі шындыққа жанасатындай болады: тербелістің спектралдық тығыздығы шекті ұзақтылығы бар тек әлдебір жиіліктер жолағы шегінде нөлден өзгешеленеді. Радиотехникада осындай сигналды шектелген спектрі бар сигнал деп атайды. Шектелген жиілік жолағы бар сигналдарды Котельников қатары түрінде көрсету. Радиотехникада сигналдар теориясы мен техникасында Котельников теоремасы (есептемелер теоремасы) негізінен қолданылады: Егер s (t) функциясы спектрінде ең жоғары жиілік fm -нен кіші болса, онда s (t) функциясы бір-бірінен секундтан аспайтын уақыт сәттеріндегі өзінің мән-дерінің тізбегімен толық анықталады. Яғни Котельников теоремасы бірдей уақыт аралықтарында алынған есептемелік мәндерін (іріктеулерін) ескере отырып шектелген спектрі бар сигналдың лездік мәндерін өте дәл қайта қалпына келтіру мүмкіндігін қарастырады. Осы теоремаға сәйкес спектрі бойынша ең жоғары жиілікпенен w m = 2p fm шектелген s (t) сигналын катар түрінде көрсетуге болады:
Осы өрнекте Осы (1) қатарда тұрған
функциясының мынандай қасиеттері бар: а) t = nDt нүктесінде jn (nDt) = 1, ал t =kD t нүктелерінде jn (kDt) = 0, мұнда k -кезкелген бүтін оң сан, немесе n -нен бөлек теріс сан; ә) jn (t) функциясының спектралдық тығыздығы ç w ç < w m жиіліктер жолағында бірқалыпты және
jn (t) функциясының j0 (t) -дан уақыт осі бойынша nDt -ға жылжу айырмашылығы болатындықтан, jn (t) функциясы спектралдық тығыздығы ì Ф = í î;0, w< - wm
3.1 – сурет. Котельников қатарымен үздіксіз сигналды аппроксимациялау Бастапқы үздіксіз сигналды дискреттелгеннен кішкентай бұрмаланулармен қайта қалпына келтіру үшін дискреттеу адымын нақты таңдап алу керек. Сондықтан аналогтық сигналды дискреттікке түрлендіргенде міндетті түрде Dt дискреттеу адымы шамасы туралы сұрақ туындайды. Егер аналогтық сигналдың, әлдебір жоғары жиілік F ж –мен шектелген төменгі жиілікті спектрі бар болса (яғни, u (t) – ның амплитудасының шұғыл өзгеріссіз жәйлап өзгеретін қисығы болатын), онда кішкентай дискреттеу уақыттық аралығы Dt –да осы функция амплитуда бойынша әжептәуір өзгеруі мүмкін. Сонымен аналогтық сигналды оның есептемелері тізбегі бойынша қайта қалпына келтіру дискреттеу интервалы шамасы Dt –ға тәуелді. Бірақ та дискреттеу уақыттық аралығы Dt кішірейген сайын аналогтық сигналды қайта қалпына келтіргенде ақпараттың бұрмалануы мен жоғалуы ықтималдығы өседі. Дискреттеу аралығынның оптималды шамасы жоғарыда келтірілген Котельников теоремасымен анықталады. Котельников қатарымен берілген бейнеленген сигналды аппаратуралық түрде синтездеуге болады. Котельников теоремасының маңызды ерекшелігі оның конструктивтік сипатында: ол сигналды сәйкесті қатарға жіктеу мүмкіндігін көрсетумен бірге, өзінің берілген есептік мәндері бойынша үздіксіз сигналды қайта қалпына келтіру әдісін де анықтайды (3.2 – сурет). Шығыс қысқыштарында есептік функцияларды Sck (t; w 0) шығаратын генераторлар жиынтығы бар дейік. Генераторлар басқарыла алады – олардың сигналдарының амплитудалары s k есептік мәндеріне пропорционал. Егер шығыстарындағы тербелістерді біріктіріп, оларды сумматорға берсек, онда сумматордың шығысында (3.1) формуласына сәйкес s (t) синтезделетін сигналдың ілездік мәндерін алуға болады. Негiзгi әдебиет:1[116-121], 2[378-381].
|

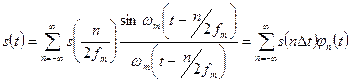 . (3.1)
. (3.1)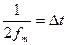 мәні уақыт осіндегі екі есептемелік нүкте арасындағы интервалды анықтайды, ал
мәні уақыт осіндегі екі есептемелік нүкте арасындағы интервалды анықтайды, ал 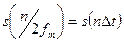 - t = nDt уақыт сәттеріндегі s (t) функциясының іріктеулері.
- t = nDt уақыт сәттеріндегі s (t) функциясының іріктеулері.
 .
. - wn <; w<wm және
- wn <; w<wm және және w>wm болғанда.
және w>wm болғанда.



