Принцип экстремума энтропии и экстремальные распределения
В ряде случаев возникает задача определения распределения вероятностей w(x) при заданных моментах случайных величин. Например, при выборе “наилучшего” распределения вероятностей при передаче сообщений или искусственно создаваемой помехи. Заданному ограничению всегда удовлетворяет бесконечное множество различных распределений вероятностей. Поэтому ставится задача выбора из данного множества некоторого наиболее подходящего распределения. В качестве критерия предлагается принцип экстремума энтропии. Данная задача решается как частная задача вариационного исчисления. При этом могут быть два случая. Первый случай при заданной дисперсии, второй - при произвольной дисперсии. Рассмотрим первый случай. Определим вид функции плотности вероятности распределения состояний элементов сообщений w(x), которая бы обеспечивала максимальную энтропию H(X) при заданной дисперсии.
При этом имеются дополнительные условия:
Для решения задачи составим уравнение Эйлера
где λ1 и λ2 - неопределенные множители;
Продифференцируем уравнение (2.7) по w(x)
Приравнивая производную нулю, получим:
Примем во внимание, что
или
Для исключения неизвестных λ1 и λ2 подставим выражение (2.8) в (2.5). Для решения полученного выражения воспользуемся табличным интегралом: Далее
Подставим (2.9) в (2.6)
При взятии интеграла учтем, что имеется соответствующий табличный интеграл Следовательно Подставим (2.10) в (2.9) и окончательно получим
В результате получили нормальный закон распределения вероятностей. Выводы: 1. Если задана дисперсия состояний сообщений, то сообщение обладает наибольшей информативностью (максимальной энтропией) в том случае, когда состояния элементов распределены по нормальному закону. 2. Если задана средняя мощность помехи, то последняя является наиболее эффективной (энтропия помехи максимальна), когда состояния составляющих помеху элементов распределены по нормальному закону. Второй случай. Определим вид функции w(x), обеспечивающей максимальную энтропию сообщений при непрерывном распределении состояний элементов и произвольной дисперсии. Эта вариационная задача имеет только одно дополнительное условие.
Решение задачи можно получить, положив в (2.7) λ2=0
тогда уравнение (2.8) будет равно Подставим в (2.12) и возьмем пределы (а - в), так как w(x) не зависит от x.
Так как функция плотности вероятности w(x) не зависит от x, то она является величиной постоянной во всем интервале существования случайной величины. Пусть состояния элементов сообщений существуют в интервале [a,b], тогда искомая функция распределения равна
внутри интервала [a,b] и нулю вне пределов его. Вывод. Если дисперсия состояний сообщений не ограничена, то сообщения обладают наибольшей информативностью (максимальной энтропией) в том случае, когда состояния элементов распределены по равновероятному закону.
|

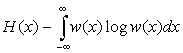
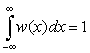 (2.5)
(2.5)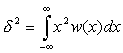 (2.6)
(2.6)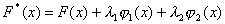 , (2.7)
, (2.7)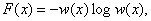
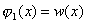 ,
, 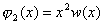 .
.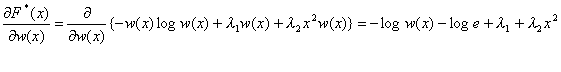
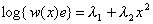
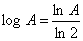 , и тогда
, и тогда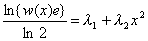 , далее
, далее 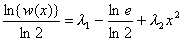 ,
,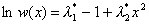 , где
, где 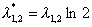
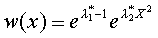 (2.8)
(2.8)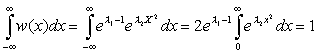
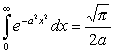
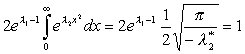
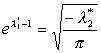 . Тогда (2.8) примет вид
. Тогда (2.8) примет вид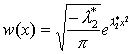 (2.9)
(2.9)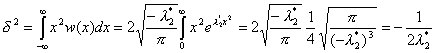
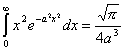
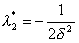 (2.10)
(2.10)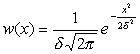 (2.11)
(2.11)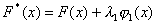
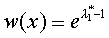
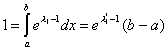 , откуда
, откуда 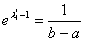
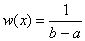 (2.13)
(2.13)


