Согласование скорости выдачи информации, выдаваемой источником, с пропускной способностью канала связи
Рассмотрим случай, когда непрерывный сигнал выдается одиночным датчиком. При этом, ширина спектра датчика равна Fd. По теореме Котельникова, найдем интервал дискретизации Пропускная способность канала связи должна быть не меньше скорости выдачи информации, выдаваемой датчиком:
Откуда Полоса пропускания канала связи должна быть тем шире, чем шире спектр передаваемой информации (то есть, чем быстрее изменяется регистрируемая величина), чем больше количество передаваемых состояний, (то есть, чем точнее производится отсчет величины, даваемой датчиком) и чем меньше допустимое в канале связи отношение сигнал/шум. Канал связи является дорогим сооружением, поэтому желательно, что бы по нему передавалась информация одновременно от многих источников информации. На рис. А представлена схема передачи информации по каналу от многих датчиков. Преобразователь служит для раздельной передачи информации, выдаваемой различными датчиками, и может быть построен с использованием метода селекции по времени или по частоте.
Рис.3.6. Комплексный датчик Учитывая, что сообщения, выдаваемые различными датчиками статистически независимые, энтропия комплексного датчика будет равна H(X)=H(X1)+H(X2)+... +H(Xn) Энтропия сообщения i-го датчика определяется суммой
где mi - количество состояний i - го датчика. Будем исходить из условий равной вероятности состояний датчиков. В этом случае энтропия будет максимальной: где m1, m2,..., mn - количество состояний 1, 2,..., n -го датчиков. Количество состояний каждого из датчиков определяет точность передаваемой информации: чем больше регистрируется состояний, тем выше точность. Будем понимать под классом точности первичных датчиков величины:
Так, если m=100, то имеем первый класс точности, при m=20 - пятый класс точности. Подставим m1, m2,..., mn в H(X)
Заменим классы точности отдельных датчиков эквивалентным классом точности комплексного датчика
Далее определяется граничная частота для датчика, работающего с наибольшей частотой Fd max. Количество опросов комплексного датчика будет Согласование комплексного датчика с каналом связи может быть достигнуто, если количество информации, даваемое таким датчиком в единицу времени, не будет превосходить пропускной способности канала связи Отсюда определяется наименьшая ширина полосы канала связи: Для передачи информации обычно применяются бинарные сигналы. Такие сигналы передаются по каналу с различной модуляцией: АМ, ФМ, ЧМ. Максимальная скорость передачи может быть определена по формуле
где F - спектр сигнала, p - вероятность искажения сигнала. Если длительность элементарного сигнала t, то F=1/t. Вероятность ложных переходов однозначно определяется через отношение P/N, поэтому можно записать
где вид функции
|

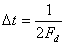 . Количество отсчетов в секунду будет составлять
. Количество отсчетов в секунду будет составлять  . Если энтропия сообщения, то есть количество информации, которое содержится в одном отсчете, равна H(X), а количество отсчетов в секунду равно n0, то количество информации, которое поступает от датчика в секунду, равно
. Если энтропия сообщения, то есть количество информации, которое содержится в одном отсчете, равна H(X), а количество отсчетов в секунду равно n0, то количество информации, которое поступает от датчика в секунду, равно 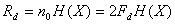 .
.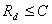 ,
, 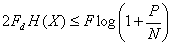 .
. (3.10)
(3.10)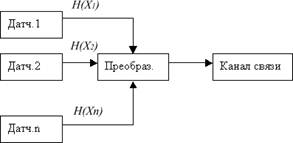
 ,
, . Тогда
. Тогда 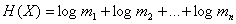 ,
,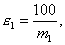
 ...,
..., 


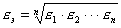
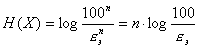
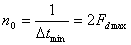 . Если количество опросов в секунду n0, то общее количество информации
. Если количество опросов в секунду n0, то общее количество информации 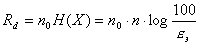 .
.
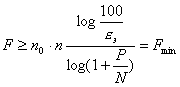 . (3.11)
. (3.11)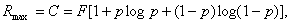
 (3.12)
(3.12)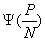 зависит от вида модуляции.
зависит от вида модуляции.


