Методы оценки опасных ситуаций
Значительное развитие и практическое применение получила теория надежности. В теории надежности исследуется вероятность отказа, то есть вероятность того, что техническое средство откажет в течение заданного времени работы. Теория надежности позволяет оценивать срок службы, по окончании которого техническое средство вырабатывает свой ресурс и должно подвергнуться капитальному ремонту, модернизации или замене.
Возможности электронно-вычислительной техники позволяют развивать метод моделирования опасных ситуаций. Моделирование оперирует формализованными понятиями. Формализации подвергаются статистические данные о происшествиях, структура и закономерности функционирования технических систем.
Практический интерес представляет построение дерева причин несчастного случая с подробным проведением анализа предшествующих событий, которые привели к нему. Достоинством такого моделирования опасностей являются простота, наглядность и легкость математической алгоритмизации. Благодаря методу можно предотвратить повторение аналогичного несчастного случая. Экстраполяционное прогнозирование. Задача оценки уровня безопасности технической системы может быть решена методом прогнозирования изменений контролируемых параметров на основе интегрального показателя безопасности. Прогнозирование контролируемых параметров технической системы осуществляется путем экстраполяции определенных на текущий момент данных. Суть экстраполяции в том, что на основе историко-фактических данных строят кривую роста того или иного показателя, характеризующего развитие технической системы, и пытаются продолжать эту кривую "в будущее".
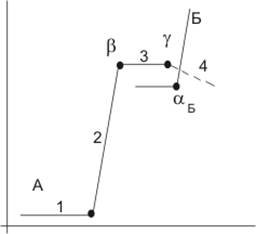
1) Метод огибающих кривых Каждая техническая система развивается сначала медленно (участок 1 на рис.), затем быстро (участок 2), после чего скорость развития снова замедляется (участок 3) и в дальнейшем начинается спад (участок 4).
Когда первая «ступенька» перестает быстро подниматься вверх, начинается подъем второй ступеньки, отражающей развитие следующей технической системы и т.д. Таким образом, хотя пределы развития конкретной технической системы ограничены, результирующая (огибающая) кривая может практически неограниченно подниматься вверх. Техника прогнозирования методом огибающих кривых проста: надо лишь правильно выбрать показатель, комплексно характеризующий развитие всей технической системы.
2) Метод наименьших квадратов
Рассмотрим подробнее нахождение уравнений регрессии для оценки изменений контролируемых параметров ТС этим методом.
Данные из таблицы (Приложение 2.) можно представить в виде п пар величин ( Этим методом находят величины А и В, минимизирующие сумму квадратов расстояний по вертикали до прямой линии
где После упрощений получаем нормальные уравнения с коэффициентами А, В.
где Найденное уравнение прямой можно также записать в виде
где x - срок эксплуатации (работы) ТС лет (задан индивидуально каждому студенту по формуле x =18+0,2К, где К – последняя цифра номера зачетной книжки). Общую оценку уровня безопасности ТС можно охарактеризовать интегральным показателем безопасности ТС
где Сi - весовой коэффициент i- го контролируемого параметра, КПi - значение i - го контролируемого параметра, KПВПДi, KПHПДi – верхнее и нижнее предельно допустимые значения i -го контролируемого параметра,
безразмерный показатель безопасности i -го контролируемого параметра, N – число контролируемых параметров.
1) Если р = 0 – безопасность ТС равна 0% (то есть уровень безопасности ТС нулевой), если р = 1 (идеал) – безопасность ТС составляет 100 %.
2) Возможно обобщение данного показателя на всю ТС, состоящую, как правило, из нескольких функционально связанных рассматриваемых элементов конструкции, что даст возможность оценивать и прогнозировать состояние безопасности ТС в целом.
3) Элемент технической системы (ТС) считается небезопасным и требующим ремонта или замены при выходе за допустимые пределы хотя бы одного из контролируемых параметров.
Подробнее о контролируемых параметрах:
Совокупность всех контролируемых параметров должна полностью характеризовать техническую безопасность исследуемого объекта и позволять оценивать прогнозируемый ресурс безопасности параметра и системы в целом. В качестве контролируемых параметров объектов повышенной опасности могут выступать:
§ геометрические параметры (диаметр, длина, толщина и т.п., причем в нескольких характерных точках);
§ физико-механические параметры (плотность, модуль упругости, предел пропорциональности, прочности материала и др.);
§ параметры, характеризующие возможные локальные ослабления исследуемой конструкции (параметры микротрещин, микроповреждений, локальных вмятин);
§ параметры, характеризующие статические эксплуатационные нагрузки, действующие на исследуемый элемент и другие группы параметров.
Контролируемые параметры могут быть получены опытным путем (измерения), расчетно-теоретическим путем (оценка нагрузок, теоретическое моделирование и т.п.), путем экспериментального определения параметров конструкции из исследуемой партии.
Пример: Рассмотрим метод наименьших квадратов на примере из таблицы:
Значения контролируемых параметров в таблице разнесены в две области: текущие данные – это данные, полученные экспериментально-теоретическим путем до текущего момента эксплуатации и прогнозируемые значения – значения, экстраполируемые по известным данным на дальнейшее время работы.
Из анализа полученных результатов следует, что к 21 году эксплуатации первый КП выходит за пределы допустимых значений. Следовательно, элемент технической системы (ТС) считается небезопасным и требующим ремонта или замены.
Порядок выполнения задания:
1) Ознакомиться с общими положениями.
2) Выписать свои исходные данные из таблицы (Приложение 2.), полученные по материалам контрольных испытаний и определить наиболее изменяющиеся параметры.
3) Рассчитать коэффициенты для уравнений регрессии для расчетов параметров методом наименьших квадратов по зависимостям (3, 5).
4) Определить прогнозируемые изменения параметров при возможной эксплуатации ТС через (18+0,2К) лет (К - последняя цифра номера зачетной книжки), используя исходные данные своего варианта табл. 3 и расчетную зависимость (6).
5) Рассчитать по определенным в пункте 3.4 прогнозируемым изменениям параметров ТС, используя расчетные зависимости (7, 8), значение интегрального показателя безопасности ТС на момент времени (18+0,2К) лет эксплуатации.
6) Построить графическую интерпретацию уравнений регрессии для каждого параметра в координатных осях – «значение параметра – время».
7) Графико-аналитическим методом определить параметры ТС для других периодов эксплуатации и заполнить таблицу 2.
8) Сделать выводы по работе:
§ определить максимальный срок безопасной эксплуатации ТС; § определить процент снижения безопасности ТС на заданный момент времени; § указать максимально возможный срок, после которого эксплуатация ТС должна быть запрещена, когда показатель безопасности р будет равен 0;
9) Оформить бланк отчета по работе (Приложение 3.).
КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Что такое техническая система? 2. Чем может быть вызвана опасность ТС? 3. Какие существуют методы оценки опасных ситуаций? 4. В чем суть экстраполяции? 5. По каким признакам определяют максимальный срок безопасной эксплуатации и максимально возможный срок эксплуатации?
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ
1. М. Добров. «Прогнозирование науки и техники», Наука, 1969. 2. Р. Эйрес. «Научно-техническое прогнозирование и долгосрочное планирование», Мир, 1971. 3. Э. Янч. «Прогнозирование научно-технического прогресса», Прогресс, 1974. 4. Гнеденко Б.В., Беляев Ю.К., Соловьев А.Д. «Математические методы в теории надежности», Наука, 2009. 5. А. Раздорожный. «Безопасность производственной деятельности», Инфа, 2002. 6. В. Шишмарев. «Надежность технических систем», Академия,2010.
|

 - параметр времени,
- параметр времени,  - значение контролируемого параметра)
- значение контролируемого параметра)  =1,..., п. Предположим, что линейная функция регрессии
=1,..., п. Предположим, что линейная функция регрессии  правильно представляет физическую ситуацию снижения безопасности объекта. Требуется найти оценки
правильно представляет физическую ситуацию снижения безопасности объекта. Требуется найти оценки  и
и  , соответственно А и В, определяющие наиболее близкую к экспериментальным точкам регрессионную прямую. Если „близость" измеряется суммой квадратов разностей между наблюдаемыми значениями Y и теми, которые дает построенная регрессионная прямая, приходим к методу наименьших квадратов.
, соответственно А и В, определяющие наиболее близкую к экспериментальным точкам регрессионную прямую. Если „близость" измеряется суммой квадратов разностей между наблюдаемыми значениями Y и теми, которые дает построенная регрессионная прямая, приходим к методу наименьших квадратов. . Определим эту сумму как
. Определим эту сумму как (1)
(1)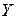 , а
, а  — величина, вычисленная с помощью построенной регрессионной прямой.
— величина, вычисленная с помощью построенной регрессионной прямой.
 (2)
(2)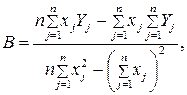 (3)
(3) (4)
(4) (5)
(5)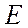
 (6)
(6) , при условии
, при условии  , (7)
, (7) _ (8)
_ (8)


