Аппроксимация данных методом наименьших квадратов
Зная отношение длин дуг находим, что градусные величины дуг АВ, ВС, CD и DA равны 60º, 80º, 100º и 120º. Вершина угла между прямыми АВ и CD лежит вне окружности, поэтому его градусная величина равна полуразности дуг AD и ВС, то есть 20º. Ответ: 20º;. Расчетно-графическая работа №2 ОБРАБОТКА РЕЗУЛЬТАТОВ НАБЛЮДЕНИЙ МЕТОДОМ НАИМЕНЬШИХ КВАДРАТОВ Цель – закрепить навыки разработки графического приложения Fortran для решения простейших инженерных задач; освоить приемы работы с выводом графика нескольких функций; изучить основы применения численной аппроксимации таблично заданных функций методом наименьших квадратов и решения систем линейных алгебраических уравнений методом исключений Гаусса. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ Аппроксимация данных методом наименьших квадратов Пусть в результате эксперимента получена таблица значений функции:
Требуется аппроксимировать эту функцию многочленом степени m (m<n):
Согласно методу наименьших квадратов (МНК) ищем значения параметров
принимает минимальное значение. С учетом необходимых условий существования экстремума функции нескольких переменных получаем систему уравнений для определения неизвестных
Доказано, что система уравнений имеет единственное решение, при котором Рассмотрим частные случаи. Случай 1. Пусть
Система уравнений для вычисления параметров
Решив систему, можем записать требуемый многочлен Случай 2. Пусть
Система уравнений для определения параметров
Решив систему, можно записать многочлен
|

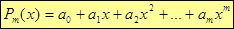 .
. , при которых сумма квадратов
, при которых сумма квадратов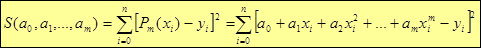

 принимает минимальное значение.
принимает минимальное значение. , т.е. функцию аппроксимируем многочленом первой степени:
, т.е. функцию аппроксимируем многочленом первой степени: .
. ,
,  имеет следующий вид:
имеет следующий вид:
 .
. , т.е. функцию аппроксимируем многочленом второй степени:
, т.е. функцию аппроксимируем многочленом второй степени: .
. имеет следующий вид:
имеет следующий вид:
 .
.


