Тема 2. Гидростатическое давление. Измерение давления
(2 часа) Гидростатика – раздел гидравлики, где изучаются законы равновесия жидкостей, действующие при этом силы плавание тел без их перемещения. Рассмотрим силы, действующие на покоящуюся жидкость. Жидкость в состоянии покоя подвергается действию двух категорий внешних сил: массовых и поверхностных. Массовые силы – силы, пропорциональные массе жидкости – это силы тяжести и силы инерции. Поверхностные силы – силы, распределенные по поверхности, ограничивающие любой мысленно выделенный объем жидкости и пропорциональные площади этой, поверхности, такие как силы давления и центробежные силы. Под действием внешних сил в каждой точке жидкости возникают внутренние силы, характеризующее её напряженное состояние называется давлением точки. Рассмотрим некоторый объем покоящейся жидкости находящейся в сосуде произвольной формы. Мысленно разделим тот объем некоторой плоскостью АВ на 2 части и отбросим верхнюю часть.
Для сохранения равновесия нижней части необходимо к плоскости АВ приложить силы, которые заменят действие верхней части объема жидкости на нижнюю. С этой целью возьмем на плоскости АВ произвольную точку К и выделяем около неё бесконечную малую площадку ω. В центре этой площадки приложения перпендикулярно плоскости АВ силу Р, представляющую собой равнодействующую всех сил, действующих в различных точках на эту плоскость. Если величину силы Р, называемую суммарной силой гидростатического давления разделить на величину площади ω, то получим среднее гидростатическое давление, на данную площадь. Рср = Если уменьшать площадку
lim ( ω → 0.
Иначе говоря, гидростатическое давление в точке является пределом отношения силы давления, действующей на элементарную площадку к её площади, если она стремится к нулю.
Гидростатическое давление обладает тремя свойствами:
1. Гидростатическое давление всегда направлено по внутренней нормами к площадке, на которую она действует. 2. Гидростатическое давление в любой точке жидкости действует одинаково по всем направлениям, т.е. не зависит о угла наклона площадки, на которую оно действует. 3. Гидравлическое давление в точке зависит только от его положения точки в пространстве. Основные уравнения в гидростатике В герметически закрытый сосуд закачен воздух до давления Р. В жидкости находящейся в состоянии покоя, выделим бесконечно малый прямоугольный параллелепипед с ребрами dx, dy, и dz,параллельными осями прямоугольных координат.
Ро – давления воздуха. Жидкость находится в состоянии покоя под действием силы тяжести и давления на свободной поверхностях. На объем жидкости действует сила давления и массовые силы (сила тяжести). На грани параллелепипеда действуют гидростатическое давление.
Px =
Py =
Pz =
Полный дифференциал гидростатического давление Р равен:
Р =
Кроме сил гидростатического давление на каждую единицу объема параллелепипеда действуют силы массы. Равнодействующую этих сил выразим через G, а её проекции, отнесенные к единице массы на соответствующие оси координат, обозначим через X, Y, Z. Уравниваем равновесие жидкости, описывающим закон распределения гидростатического давления является дифференциальное уравнение гидростатики:
Выделим в объеме точку М. На частицу жидкости, находящуюся в точке М действуют силы тяжести, определенные по формуле mg при массе частицы жидкости в т. М равной 1 проекции сил будут равны x = 0, y = 0, z = -g. Тогда уравнение 1 можно представить в виде Объем единицы массы удельный объем жидкости, поэтому γ – удельный вес Разделив обе части уравнения на
Теперь проинтегрируем уравнение и получим:
Постоянную интегрирования найдем из граничных условий, при Z = zo; P=Po
Приравняем формулы 2 и 3 и получим:
Решая уравнение 4 относительно Р, предполагая, что
P = где h – высота столба жидкости
Это уравнение описывает условие равновесия жидкости как под действием силы тяжести так и под влиянием внешнего давления и называется основным уравнением гидростатики. Полученное уравнение можно сформулировать так: абсолютное или полное давление в любой точке покоящейся жидкости слагается из давление на свободной поверхности Ро и давления, определенного весом столба жидкости
|

 , [Па]
, [Па]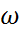 то среднее гидростатическое давление будет стремиться к некоторому пределу, выражающему гидростатическое давление в данной точке
то среднее гидростатическое давление будет стремиться к некоторому пределу, выражающему гидростатическое давление в данной точке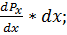
 ;
;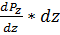
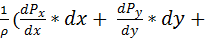
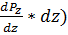
 ) (1)
) (1) , но
, но 
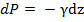
 и перенесем влево, получим:
и перенесем влево, получим:
 (2)
(2)
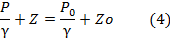
 , будем иметь:
, будем иметь: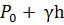 (5)
(5)



