Наближені обчислення
Важливим питанням є те, скільки значущих цифр слід зберігати в результаті кожної дії. Точність обчислень результатів вимірювання має відповідати точності вимірювань. Виконувати обчислення з точністю, більшою ніж це дозволяють експериментальні дані, нераціонально і некоректно. Отже, обчислення, які виконуються при математичній обробці експериментальних результатів, отриманих у науковій чи навчальній лабораторії, є наближеними. Одержані числа можна округляти, тобто зменшувати кількість їх значущих цифр. Щоб округлити число до n значущих цифр, треба відкинути усі цифри, які стоять після n-го розряду. При цьому користуються такими правилами: якщо перша з цифр, які відкидають менша 5, то остання з тих цифр, які залишаються, не змінюється; якщо ж перша з цифр, які відкидають, більша або рівна 5, то остання цифра, з тих цифр, які зберігаються, збільшується на одиницю. Наприклад, округлення числа 7,192 до трьох значущих цифр дає число 7,19, до двох 7,2. Округлення числа 1681 до двох значущих цифр дає число У наближених обчисленнях записи 25,6 і 25,600 відрізняються один від одного. У числі 25,6 точні (правильні) лише цифри цілих і їхні десяті частини, а в числі 25,600 також соті і тисячні частини. Прийнято вважати, що k -та цифра наближеного числа а точною (правильною), якщо абсолютна похибка цього числа не перевищує половини одиниці k-го розряду цієї цифри. Всі цифри, які стоять лівіше від правильної, також правильні. У протилежному випадку цифру k-го розряду називають сумнівною. Сумнівною цифрою називають ту, яка стоїть безпосередньо за крайньою справа правильною цифрою. Цифри, які стоять справа від сумнівної цифри, називаються неправильними. Неправильні цифри повинні бути відкинуті шляхом округлення як у вихідних даних, так і у кінцевому результаті розрахунку. Всі правильні цифри числа, починаючи з першої зліва, відмінної від нуля, і включаючи першу сумнівну цифру, називаються значущими цифрами. Всі інші цифри називаються незначущими. Наприклад, у числі 0,0507 три значущих цифри; перші два нулі незначущі, нуль між п’ятіркою і семіркою – значущий. Записуючи остаточні результати наближених обчислень, незначущі цифри числа відкидають. У числі 2500 – чотири значущих цифри (нулі в числі 2500 – значущі цифри; точно відомо, що одиниць і десятків у числі 2500 немає). Запис 47200·103 або 0,47200·108 означає, що в числі 47 200 000 три останні цифри не значущі, а всі інші – значущі. Запис результатів вимірювання має відповідати також точності вимірювання. Наприклад, якщо товщина пластинки після обчислень становить 4,5568 мм при абсолютній похибці вимірювання 0,02 мм, то такий запис числа не відповідає теорії похибок вимірювання. Середнє арифметичне значення для товщини пластинки в цьому разі слід округлити до 4,56 мм. Взагалі при округленні наближеного або точного числа а до n значущих цифр за правилом доповнення число а замінюють числом Якщо з наближеними числами ще проводитимуться обчислення, то в них слід зберігати одну або дві сумнівні цифри. При виконанні математичних операцій над наближеними числами слід дотримуватись таких правил. Наближені числа треба округляти перед виконанням відповідних математичних операцій. Округляти числа слід за наведеним вище правилом до розряду найменш точного числа, залишаючи в числах одну або дві запасні цифри. Це дає змогу цілком правильно округлити кінцевий результат. У кінцевому результаті ці «запасні» цифри відкидають. При додаванні і відніманні наближених чисел кінцевий результат слід округляти так, щоб у ньому не було значущих цифр у тих розрядах, яких немає хоча б в одному з наближених чисел. Наприклад: 5,962 + 2,49 + 7,18376 + 6,1468 При множенні і діленні наближених чисел у кінцевому результаті слід залишати стільки значущих цифр, скільки їх є в наближеному числі з найменшою кількістю значущих цифр. Наприклад: 3,624·2,4·5,1127·3,62·2,4·5,11=8,688 При піднесенні до степеня в кінцевому результаті слід залишити стільки значущих цифр, скільки їх має наближене число, яке підноситься до степеня. Наприклад: (1,26)2=3,276 При добуванні коренів у кінцевому результаті слід залишити стільки значущих цифр, скільки їх має підкореневе наближене число. Наприклад: Знаходячи логарифм наближеного числа, потрібно брати з таблиць чи з дисплея мікрокалькулятора для мантиси стільки значущих цифр, скільки їх має це число. Наприклад: lg77,23 Правильне і обернене: число, яке знаходять за логарифмом, повинно мати стільки значущих цифр, скільки їх у мантиси (при довільній характеристиці). На основі викладеного вище, сформулюємо правила запису вимірювань і розрахунків, яких слід дотримуватись у навчальній лабораторії: 1. Остаточні результати вимірювань і розрахунків записують разом з їх абсолютною похибкою. 2. При запису похибок обмежуються однією (інколи двома значущими цифрами). Остання цифра результатів і остання цифра його абсолютної похибки повинні належати до одного і того ж самого десятинного розряду. Приклад правильного запису: 3..Якщо в похибці перша значуща цифра одиниця, то після неї зберігається ще одна, а в результаті дві сумнівні цифри. Приклад правильного запису: 4. Якщо у відповіді міститься множник виду 10n, то і у результаті, і у його абсолютній похибці він повинен бути однаковим. Приклад правильного запису: 5. Вимірювана величина і її абсолютна похибка виражаються в одних одиницях вимірювань. Приклад правильного запису: 6. Абсолютна похибку також треба округляти до однієї (іноді до двох) значущих цифр. Детальніше ознайомитись з методами обробки експериментальних результатів і розрахунку похибок можна за посібниками [7-9,11,19,39,40,43-46].
|

 , а округлення числа 0,80214 – число 0,8. Абсолютна похибка округленого числа не перевищує половини одиниці останньої збереженої цифри. Це, зокрема, слід враховувати при округленні табличних даних та значень фізичних сталих, які беруть з довідкових таблиць.
, а округлення числа 0,80214 – число 0,8. Абсолютна похибка округленого числа не перевищує половини одиниці останньої збереженої цифри. Це, зокрема, слід враховувати при округленні табличних даних та значень фізичних сталих, які беруть з довідкових таблиць. з n значущими цифрами так, щоб похибка округлення не перевищувала половини одиниці розряду, що зберігається.
з n значущими цифрами так, щоб похибка округлення не перевищувала половини одиниці розряду, що зберігається. 5,962+2,49+7,184 + +6,147=21,783
5,962+2,49+7,184 + +6,147=21,783  .
. Приклад неправильного запису:
Приклад неправильного запису: 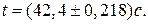
 . Приклад неправильного запису:
. Приклад неправильного запису:  .
. . Приклад неправильного запису:
. Приклад неправильного запису:  .
. . Приклад неправильного запису
. Приклад неправильного запису  .
.


