Визначення модуля Юнга сталі статичним методом за деформацією розтягу
Мета лабораторної роботи: Визначення модуля Юнга сталі статичним методом за деформацією розтягу дротини.
Деякі теоретичні відомості
Усі тверді тіла під дією сил деформуються, тобто змінюють об’єм і форму. Розрізняють деформації розтягу, стиску, зсуву, кручення, згину (три останні зводяться до суперпозиції двох перших). Якщо деформації зникають після припинення дії прикладених зовнішніх сил, то вони називаються пружними. Деформації, які зберігаються після припинення дії зовнішніх сил, називаються пластичними. Розділення деформацій на пружні і пластичні є умовним, оскільки після дії будь якої сили у реальному твердому тілі залишаються остаточні деформації. Але якщо вони є дуже малими, то деформації вважають пружними. Для пружних тіл між діючими силами і викликаними ними деформаціями існує однозначна залежність (при пластичних деформаціях такої однозначності немає). Як показали експериментальні дослідження, малі пружні деформації тіл прямо пропорційні зовнішнім силам, які їх спричинили. Якщо тіло знаходиться у рівновазі, то це означає що зовнішні сили зрівноважені пружними силами, які виникли у тілі внаслідок його деформації. Ці сили намагаються надати тілу попередніх розмірів і форми. Встановлено, що для багатьох твердих тіл існують області малих пружних деформацій (різні у кожному випадку). Кількісною мірою, яка характеризує ступінь деформації, є відносна деформація, яка визначається відношенням абсолютної деформації до величини, яка характеризує вихідні розміри і форму тіла. Одним із типів пружних деформацій є деформація розтягу. Розглянемо деформацію розтягу на прикладі однорідного ізотропного зразка, наприклад стрижня довжиною
Рис.1
До кінців стрижня прикладені направлені вздовж його осі рівні сили
Якщо сила направлена до нормалі до поверхні, то напруження називається нормальним Під дією сил, стрижень пружно деформується, у результаті чого, його довжина змінюється на величину
Одночасно з деформацією розтягу стрижня, яка характеризується його відносним видовженням Відповідно до закону Гука напруження пружної деформації розтягу пропорційне відносному видовженню стрижня:
де Поклавши у виразі (3) Розглянемо діаграму напружень, яка на якісному рівні відображає залежність між прикладеним напруженням і відносним видовженням металічного зразка.
Рис.2
Аналізуючи цей графік можна зробити висновок щодо того, що лінійна залежність між Для експериментального визначення модуля Юнга певного матеріалу може бути використаний поздовжній розтяг дротини, виготовленої з цього матеріалу. Дротина циліндричної форми, початкової довжини
де коефіцієнт пропорційності Якщо змінюючи навантаження дротини
Опис експериментальної установки.
Рис.3
Схему установки, призначеної для визначення модуля Юнга за деформацією розтягу, наведено на рис.3. Стальна дротина 1 розтягується під дією змінних вантажів, вагою
Порядок виконання роботи.
1. Визначте ціну поділки катетометра. Для цього сумістіть візирний хрест, або один з штрихів вертикальної шкали окуляра зорової труби катетометра (так звану реперну точку) з одним із штрихів вертикально поставленої еталонної лінійки і відлічіть показання на основній вертикальній шкалі та на лімбі катетометра. Повертаючи лімб, перемістіть зорову трубу катетометра так, щоб на візирний хрест або вибраний для вимірювань один з штрихів окулярної шкали змістився на декілька міліметрів. Після цього знову відлічіть показання за основною шкалою та за лімбом катетометра. Різниця результатів цих двох відліків дає вертикальне переміщення реперної точки в поділках катетометра n. Поділивши переміщення реперної точки за шкалою еталонної лінійки в міліметрах на переміщення, виражене в поділках катетометра, отримайте ціну поділки катетометра у міліметрах. 2. Виміряйте в кількох місцях і у різних (наприклад у взаємно перпендикулярних напрямах) діаметр дротини d та визначте його середнє значення. 3. Виміряйте ефективну довжину дротини 4. Навантажуючи платформу спочатку одним вантажем маси 5. Розвантажуючи платформу, тобто знімаючи з неї по одному вантажі маси 6. За отриманими даними обчисліть відносне видовження дротини та нормальне напруження. 7. Побудуйте графік залежності відносного видовження дротини від нормального напруження. 8. За нахилом цього графіка визначте модуль Юнга. Розрахуйте відносну і абсолютну похибки, з якими ви визначили цей модуль пружності. Порівняйте одержане значення Е з табличним значенням величини модуля Юнга сталі, яке наведено у довідковій таблиці у Додатку №4. Зробіть висновки. Таблиця №1
Література: [1-15,19-38,47] Лабораторна робота №9
|

 (рис.1).
(рис.1).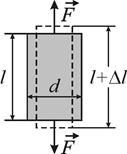
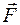 . Пружну силу, яка діє на одиницю площі поперечного перерізу тіла, називається напруженням (механічним напруженням). Модуль цієї сили визначається за формулою:
. Пружну силу, яка діє на одиницю площі поперечного перерізу тіла, називається напруженням (механічним напруженням). Модуль цієї сили визначається за формулою: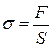 . (1)
. (1)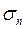 , а якщо воно направлене по дотичній до поверхні, то дотичним (тангенціальним)
, а якщо воно направлене по дотичній до поверхні, то дотичним (тангенціальним) 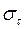 .
. . Відносна деформація стрижня
. Відносна деформація стрижня  , яка у даному випадку називається відносним видовженням, визначається за формулою
, яка у даному випадку називається відносним видовженням, визначається за формулою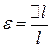 . (2)
. (2) відбувається зменшення його поперечних розмірів, яке характеризується відносною поперечною деформацією
відбувається зменшення його поперечних розмірів, яке характеризується відносною поперечною деформацією  .
.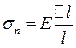 , (3)
, (3) - модуль пружності, який залежить від речовини, з якої виготовлено стрижень, і його фізичного стану. Цей модуль був уведений англійським вченим Т. Юнгом і носить його ім’я.
- модуль пружності, який залежить від речовини, з якої виготовлено стрижень, і його фізичного стану. Цей модуль був уведений англійським вченим Т. Юнгом і носить його ім’я. , знайдемо, що модуль Юнга чисельно дорівнює напруженню, яке виникло б у разі збільшення довжини досліджуваного зразка (у даному випадку довжини стрижня) у 2 рази за інших незмінних умов. Насправді майже всі матеріали руйнуються (розриваються) раніше, ніж вони будуть видовжені вдвічі (виняток – гума). Величина
, знайдемо, що модуль Юнга чисельно дорівнює напруженню, яке виникло б у разі збільшення довжини досліджуваного зразка (у даному випадку довжини стрижня) у 2 рази за інших незмінних умов. Насправді майже всі матеріали руйнуються (розриваються) раніше, ніж вони будуть видовжені вдвічі (виняток – гума). Величина  називається коефіцієнтом пружності при деформації розтягу. Вона є пружною характеристикою матеріалу, з якого виготовлено стрижень.
називається коефіцієнтом пружності при деформації розтягу. Вона є пружною характеристикою матеріалу, з якого виготовлено стрижень.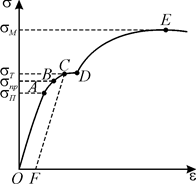
 і
і  , встановлена Гуком, виконується лише в певних вузьких межах до межі пропорційності
, встановлена Гуком, виконується лише в певних вузьких межах до межі пропорційності  . При подальшому збільшенні напруження деформація є ще пружною, хоч залежність між
. При подальшому збільшенні напруження деформація є ще пружною, хоч залежність між  остаточні деформації у тілі ще не виникають. За межею пружності в тілі виникають остаточні деформації і графік, який описує повернення тіла у вихідний стан після припинення дії сили, зображується не кривою ВО, а паралельною їй кривою CF. Напруження, при якому проявляється помітна остаточна деформація
остаточні деформації у тілі ще не виникають. За межею пружності в тілі виникають остаточні деформації і графік, який описує повернення тіла у вихідний стан після припинення дії сили, зображується не кривою ВО, а паралельною їй кривою CF. Напруження, при якому проявляється помітна остаточна деформація 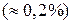 , називається межею текучості (
, називається межею текучості ( ) У області: СD – тіло ніби «тече». Ця область називається областю текучості (або областю пластичних деформацій). При подальшому розтягу (за точку D) напруження спочатку різко збільшується, а потім зменшується і здійснюється руйнування тіла. Максимальне напруження, яке виникає у тілі до руйнування, називається межею міцності (
) У області: СD – тіло ніби «тече». Ця область називається областю текучості (або областю пластичних деформацій). При подальшому розтягу (за точку D) напруження спочатку різко збільшується, а потім зменшується і здійснюється руйнування тіла. Максимальне напруження, яке виникає у тілі до руйнування, називається межею міцності ( ).
).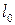 , і діаметра
, і діаметра  , яка виготовлена з досліджуваного матеріалу, розтягується під дією вантажу
, яка виготовлена з досліджуваного матеріалу, розтягується під дією вантажу  . Площа поперечного перерізу дротини
. Площа поперечного перерізу дротини  , а нормальне напруження
, а нормальне напруження 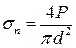 . Закон Гука у цьому випадку можна представити у вигляді
. Закон Гука у цьому випадку можна представити у вигляді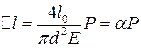 , (4)
, (4)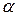 - практично постійна для даного зразка величина.
- практично постійна для даного зразка величина. і розраховувати нормальне напруження
і розраховувати нормальне напруження  , яке його спричинило, то можна побудувати графік залежності
, яке його спричинило, то можна побудувати графік залежності  . За нахилом цього графіка можна визначити модуль Юнга. Отже
. За нахилом цього графіка можна визначити модуль Юнга. Отже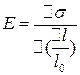 . (5)
. (5)
 які поміщуються на платформу 2. Довжина дротини вимірюється рулеткою, а її діаметр – мікрометром. Абсолютне видовження дротини вимірюють за допомогою катетометра 3, спостерігаючи у зорову трубу катетометра за вертикальним зміщенням горизонтальної мітки, закріпленої на дротині, яке відбувається при навантаженні (розвантаженні) дротини.
які поміщуються на платформу 2. Довжина дротини вимірюється рулеткою, а її діаметр – мікрометром. Абсолютне видовження дротини вимірюють за допомогою катетометра 3, спостерігаючи у зорову трубу катетометра за вертикальним зміщенням горизонтальної мітки, закріпленої на дротині, яке відбувається при навантаженні (розвантаженні) дротини. , а потім додаючи по одному ще два вантажі і, тим самим, послідовно збільшуючи навантаження дротини, визначте за допомогою катетометра не менше ніж по три рази абсолютне видовження дротини у поділках катетометра
, а потім додаючи по одному ще два вантажі і, тим самим, послідовно збільшуючи навантаження дротини, визначте за допомогою катетометра не менше ніж по три рази абсолютне видовження дротини у поділках катетометра  . Результати досліджень запишіть у таблицю №1.
. Результати досліджень запишіть у таблицю №1. ,
у по-діл-ках
,
у по-діл-ках
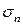 ,
Па
,
Па



