Визначення модуля зсуву сталі статичним методом за деформацією кручення
Мета лабораторної роботи: Визначення модуля зсуву сталі статичним методом за деформацією кручення стрижня. Деякі теоретичні відомості Зсувом називається така деформація твердого тіла, при якій всі його плоскі шари, паралельні деякій площині, яка називається площиною зсуву, не викривляючись і не змінюючись у розмірах, зміщуються паралельно один одному. При зсуві об’єм твердого тіла не змінюється.
Рис.1 Розглянемо деформацію зсуву на прикладі пружної деформації твердого тіла, яке має форму паралелепіпеда (рис.1). Основу паралелепіпеда, тобто його нижню грань, закріпимо нерухомо, а в площині верхньої грані прикладемо по дотичній довільної величини силу
де
Отже, модуль зсуву, в межах пружності, дорівнює дотичному напруженню, яке виникло б у зразку при відносному зсуві, що дорівнює одиниці. Модуль зсуву експериментально іноді визначають із деформації кручення, оскільки цю деформацію можна описати тими ж параметрами, які характеризують деформацію зсуву. Якщо основу 1 циліндричного стрижня закріпити нерухомо (рис.2), а до іншої основи 2 прикласти пару сил, то в стрижні виникає деформація кручення. Момент
Рис.2 Закон Гука для деформації кручення матиме такий вигляд:
де У результаті деформації кручення відбувається деякий перекіс твірної циліндра на кут
З трикутника ВАА′ при малому куту
Прирівнявши обидві частини рівнянь (4) і (5), одержимо таке рівняння:
Отже, з (6) видно, що деформацію кручення можна виразити через деформацію зсуву і навпаки. Відомо, що модуль кручення
Підставимо вираз (7) у (3), одержимо
З формули (8) знаходимо модуль зсуву
Для експериментального визначення модуля зсуву у даній лабораторній роботі використовують статичний метод.
Опис експериментальної установки та методики вимірювань.
Прилад для визначення модуля зсуву складається з рами на якій закріплена муфта для фіксації стального стрижня (на рис.3 вона не показана) і диска D, радіус якого R. Диск прикріплений до нижнього кінця стрижня, який підвішений на рамі, Верхній кінець стрижня затиснутий у муфті гвинтом. На диск намотаний шнур в одному напрямі і до його кінців, перекинутих через блоки, прикріплені шальки для тягарців. Якщо на шальки покласти однакової маси тягарці, то обертальний момент
де n та n0 – показання шкали відповідно при навантаженій певним вантажем та при ненавантаженій ним установці; d – відстань від дзеркала Z до шкали зорової труби. З формул (9) і (10) одержимо робочу формулу для визначення модуля зсуву
Порядок виконання роботи.
1. Виміряйте довжину L стрижня (відстань між місцями закріплення стрижня на рамі та на диску), діаметр стрижня r (в декількох місцях та обчисліть його середнє значення), радіус диска R та відстань від дзеркала до шкали d. 2. Поступово збільшуючи, а потім зменшуючи момент прикладених сил, зафіксуйте, використовуючи суб’єктивний метод дзеркала і шкали, відповідні кути закручування стрижня
де m – маса вантажу на одній платформі; g – прискорення вільного падіння. 3. Розрахуйте за формулою (11), підставляючи у неї відповідні значення моментів пари сил, модуль зсуву 4. Обчисліть середнє значення модуля зсуву Таблиця №1
Література: [1-9,11,20-38,47] Лабораторна робота №11
|

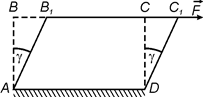
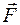 . Під дією цієї сили грані паралелепіпеда перекосяться і тому горизонтальні шари тіла зсунуться один відносно одного. Прямокутна грань АВСD після його деформації зсувом стає паралелограмом АВ′С′D, а бічні грані тіла зміщуються на кут
. Під дією цієї сили грані паралелепіпеда перекосяться і тому горизонтальні шари тіла зсунуться один відносно одного. Прямокутна грань АВСD після його деформації зсувом стає паралелограмом АВ′С′D, а бічні грані тіла зміщуються на кут  . Кут
. Кут 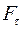 і обернено пропорційно площі поперечного перерізу
і обернено пропорційно площі поперечного перерізу 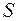 . Крім того, кут
. Крім того, кут  , (1)
, (1)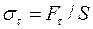 - тангенційне (дотичне) напруження, а
- тангенційне (дотичне) напруження, а  - модуль зсуву. Якщо в рівнянні (1) покласти
- модуль зсуву. Якщо в рівнянні (1) покласти  , то воно набере такий вигляд
, то воно набере такий вигляд . (2)
. (2) пари сил відносно осі
пари сил відносно осі 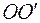 стрижня направлений вздовж цієї осі. Під дією обертального моменту
стрижня направлений вздовж цієї осі. Під дією обертального моменту  . Кут
. Кут 
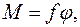 (3)
(3)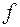 - модуль кручення. Величина модуля кручення залежить не тільки від природи матеріалу, з якого виготовлено тіло. Значення цього модуля залежить також і від геометричної форми тіла, яке деформується.
- модуль кручення. Величина модуля кручення залежить не тільки від природи матеріалу, з якого виготовлено тіло. Значення цього модуля залежить також і від геометричної форми тіла, яке деформується. . (4)
. (4)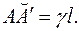 (5)
(5) (6)
(6)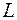 дорівнює
дорівнює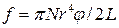 (7)
(7)
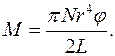 (8)
(8) (9)
(9)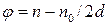 , (10)
, (10)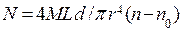 . (11)
. (11) і
і  треба брати їх середні арифметичні значення. За кут закручування, який відповідає тому чи іншому вантажу, треба брати середнє арифметичне із різниць показань шкали, одержаних при вимірювання, проведених в одному (при навантажені вантажем) і у другому (при розвантажені вантажем) напрямку. Моменти пари сил створюйте розташовуючи почергово на платформах попарно рівні вантажі маси
треба брати їх середні арифметичні значення. За кут закручування, який відповідає тому чи іншому вантажу, треба брати середнє арифметичне із різниць показань шкали, одержаних при вимірювання, проведених в одному (при навантажені вантажем) і у другому (при розвантажені вантажем) напрямку. Моменти пари сил створюйте розташовуючи почергово на платформах попарно рівні вантажі маси 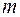

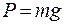 , (12)
, (12) . Розрахуйте абсолютну та відносну похибки. Порівняйте одержане значення з табличним значенням модуля зсуву сталі, яке наведене у довідковій таблиці Додатку №4.
. Розрахуйте абсолютну та відносну похибки. Порівняйте одержане значення з табличним значенням модуля зсуву сталі, яке наведене у довідковій таблиці Додатку №4. , м
, м
 ,
м
,
м



