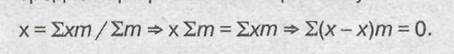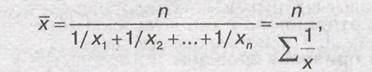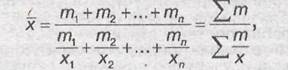Средняя величина как обобщающая характеристика совокупности. Научные принципы расчета средних величин.

Метод средних величин является одним из наибо­лее важных методов в статистике, потому что средние величины широко используются в анализе, на практи­ке, при установлении закономерностей тенденций, связей и для множества других целей. Суть средних величин состоит в том, что они одним числом характе­ризуют уровень исследуемого признака. Отличитель­ной особенностью средних величин является то, что они представляют собой обобщающие показатели.

Средняя величина — это обобщающий показа­тель, выражающий типичный уровень (размер) варьи­рующего признака в расчете на единицу совокупно­сти (качественно однородной).

Средняя величина отражает то общее, что скры­вается в каждой единице совокупности. Она улавли­вает общие черты, общие закономерности, которые проявляются в силу закона больших чисел. Говоря о средних величинах, имеют в виду, что они характе­ризуют всю совокупность в целом, однако, наряду со средней необходимо приводить данные об отдельных единицах совокупности.

Задачи, решаемые с помощью метода средних величин:

1) характеристика уровня развития исследуемого яв­ления;

2) сравнение двух или нескольких уровней иссле­дуемых совокупностей;

3) характеристика изменения уровня явления во вре­мени;

4) выявление и характеристика связей между иссле­дуемыми совокупностями.

Принципы построения средних величин:

1) средние величины могут быть рассчитаны только лишь для качественно однородных совокупностей;

2) средние величины не должны быть абстрактными, т.е. только количественными показателями. Они должны давать качественно-количественную ха­рактеристику исследуемому явлению. Поэтому в статистике средняя величина представляет со­бой не абстрактное, отвлеченное число, а вполне конкретный показатель, относимый к какому-либо явлению, месту, времени;

3) выбор единицы совокупности, по отношению к ко­торой рассчитывается средняя величина, должен быть теоретически обоснован.

Выделяются следующие основные виды средних вели­чин: средняя арифметическая; средняя гармоническая; средняя квадратическая; средняя геометрическая.

Перечисленные средние (кроме средней геометрической) объединяются в общей формуле средней степенной (при различной величине k):

 

 

где х - средняя величина исследуемого явления;

х_i – i -й вариант осредняемого признака (i = 1, n);

f_i - вес i -гo варианта.

Помимо степенных средних в статистической практике также ис­пользуются средние структурные, среди которых наиболее распрост­ранены мода и медиана.

 

14. Средняя арифметическая: простая и взвешенная.

 

Основной средней величиной является средняя арифметическая. Выделяют простую и взвешен­ную среднюю арифметическую.

Базой для расчета простой средней арифметиче­ской являются первичные записи результатов наблю­дения. Предположим, что известны значения призна­ка х₁, х₂.....х_т. Каждое из этих значений повторяется один раз (или теоретически одинаковое количество раз), т.е. данные не сгруппированы. Тогда для такого ряда следует использовать формулу средней ариф­метической простого ряда или простую среднюю арифметическую:

где х — значение варьирующегося признака; п — число единиц совокупности. Базой для расчета взвешенной средней арифмети­ческой является обработанный цифровой материал, т.е. сгруппированные данные. Для таких данных использу­ется формула средней арифметической взвешенной:

где х — значение варьирующегося признака;

т — веса, т.е. частоты, показывающие, сколько раз повторяется каждое значение признака в дан­ной совокупности. Формула получена путем взве­шивания значений каждой варианты и деления суммы вариант на сумму весов. Формулы простой и взвешенной средней арифме­тической не эквивалентны друг другу.

Свойства средней арифметической:

1) алгебраическая сумма отклонений всех вариантов от средней арифметической равна нулю:

Это свойство используется для проверки правиль­ности расчетов;

2) сумма квадратов отклонений вариант от их сред­ней арифметической больше суммы квадратов отклонений вариант от любого другого числа, не рав­ного средней арифметической:

3) среднее алгебраическое суммы нескольких варьи­рующихся признаков равно сумме средних этих признаков:

Это свойство позволяет определить сумму путем суммирования значений каких-либо признаков;

4) если все варианты (х) увеличить или уменьшить на какое-либо постоянное число (а), средняя (х) уве­личится или уменьшится на то же самое число (у):

5) если все варианты (х) увеличитьили уменьшить в од­но и то же число раз (в), то средняя арифметическая увеличится или уменьшится вто же самое число раз:

 

15. Средняя гармоническая: простая и взвешенная.

При решении задач расчет средней величины на­чинается с составления исходного отношения — ло­гической словесной формулы средней. Она состав­ляется на основе теоретического и логического анализа. Иногда среднюю арифметическую нельзя использовать. В этом случае в зависимости от ситуа­ции применяется одна из трех форм средней – средняя гармоническая, средняя квадратическая или средняя геометричекая.

Средняя гармоническая простая строится по формуле:

где n —число единиц совокупности или число вариантов; х —значения варьирующегося признака.

Средняя гармоническая простая используется для несгруппированных данных.

Средняя гармоническая взвешенная строится по формуле:

Где х – значения варьирующего признака; m – веса; n – число единиц совокупности.