МАТРИЧНЫЙ МЕТОД РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
Матрицы дают возможность кратко записать систему линейных уравнений. Пусть дана система из 3-х уравнений с тремя неизвестными:
Рассмотрим матрицу системы Найдем произведение
т.е. в результате произведения мы получаем левые части уравнений данной системы. Тогда пользуясь определением равенства матриц данную систему можно записать в виде
Здесь матрицы A и B известны, а матрица X неизвестна. Её и нужно найти, т.к. её элементы являются решением данной системы. Это уравнение называют матричным уравнением. Пусть определитель матрицы отличен от нуля |A| ≠ 0. Тогда матричное уравнение решается следующим образом. Умножим обе части уравнения слева на матрицу A-1, обратную матрице A: Заметим, что поскольку обратную матрицу можно найти только для квадратных матриц, то матричным методом можно решать только те системы, в которых число уравнений совпадает с числом неизвестных. Однако, матричная запись системы возможна и в случае, когда число уравнений не равно числу неизвестных, тогда матрица A не будет квадратной и поэтому нельзя найти решение системы в виде X = A-1B. Примеры. Решить системы уравнений. Пример 1.
Найдем матрицу обратную матрице A.
Таким образом, x = 3, y = – 1. Пример 2.
Итак, х1=4,х2=3,х3=5. Пример 3. Решите матричное уравнение: XA+B=C, где Выразим искомую матрицу X из заданного уравнения.
Найдем матрицу А-1.
Проверка:
2. ПРОВЕРКА НА СОВМЕСТНОСТЬ СИСТЕМЫ С ПОМОЩЬЮ ТЕОРЕМЫ КРОНЕКЕРА - КАПЕЛЛИ И РЕШЕНИЕ СИСТЕМ m ЛИНЕЙНЫХ УРАВНЕНИЙ С n НЕИЗВЕСТНЫМИ. Как было сказано выше, матричный метод и метод Крамера применимы только к тем системам линейных уравнений, в которых число неизвестных равняется числу уравнений. Далее рассмотрим произвольные системы линейных уравнений. Определение. Система m уравнений с n неизвестными в общем виде записывается следующим образом:
где aij – коэффициенты, а bi – постоянные. Решениями системы являются n чисел, которые при подстановке в систему превращают каждое ее уравнение в тождество. Определение. Если система имеет хотя бы одно решение, то она называется совместной. Если система не имеет ни одного решения, то она называется несовместной. Определение. Система называется определенной, если она имеет только одно решение и неопределенной, если более одного. Определение. Для системы линейных уравнений матрица А =
А*= Определение. Если b1, b2, …,bm = 0, то система называется однородной. однородная система всегда совместна, т.к. всегда имеет нулевое решение. Элементарные преобразования систем. К элементарным преобразованиям относятся: 1)Прибавление к обеим частям одного уравнения соответствующих частей другого, умноженных на одно и то же число, не равное нулю. 2)Перестановка уравнений местами. 3)Удаление из системы уравнений, являющихся тождествами для всех х.
Теорема Кронекера – Капелли. (условие совместности системы) (Леопольд Кронекер (1823-1891) немецкий математик) Теорема: Система совместна (имеет хотя бы одно решение) тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы. RgA = RgA*. Очевидно, что система (1) может быть записана в виде: x1 Если RgA = RgA*, то это означает, что они имеют один и тот же базисный минор. Столбец свободных членов – линейная комбинация столбцов базисного минора, те верна запись, приведенная выше. Пример 1. Определить совместность системы линейных уравнений:
A =
~ A* = Система несовместна.
Пример 2. Определить совместность системы линейных уравнений.
A* =
RgA = RgA*. Система совместна.
Решения: x1 = 1; x2 =1/2.
|


 и матрицы столбцы неизвестных и свободных членов
и матрицы столбцы неизвестных и свободных членов 
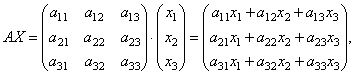
 или короче A∙X=B.
или короче A∙X=B. . Поскольку A-1A = E и E∙X = X, то получаем решение матричного уравнения в виде X = A-1B.
. Поскольку A-1A = E и E∙X = X, то получаем решение матричного уравнения в виде X = A-1B.
 ,
, 





 ,
, называется матрицей системы, а матрица
называется матрицей системы, а матрица называется расширенной матрицей системы
называется расширенной матрицей системы + x2
+ x2  + … + xn
+ … + xn 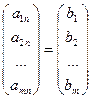
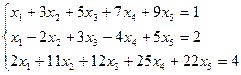
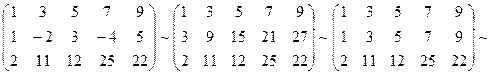
 .
.  RgA = 2.
RgA = 2. RgA* = 3.
RgA* = 3. А =
А =  ;
;  = 2 + 12 = 14 ¹ 0; RgA = 2;
= 2 + 12 = 14 ¹ 0; RgA = 2;
 RgA* = 2.
RgA* = 2.



