Вычисление двойного интеграла в декартовой системе координат.
При вычислении двойного интеграла разбиение области D удобно проводить прямыми x=const; y=const, тогда очевидно, что @
Пусть функция z=f(x;y) определена и непрерывна в некоторой области @ Рассмотрим область D специального вида:
Поставим задачу нахождения объёма цилиндроида с основанием Vцил. = Возьмем произвольное Vцил. = Из последних формул имеем:@ или @
Вывод: Вычисление двойного интеграла сводится к вычислению двух обыкновенных определенных интегралов (повторное интегрирование). Вычисление повторного интеграла: 1. Вначале вычисляют внутренний интеграл. В этом интеграле переменной считают величину y, а x – фиксированной величиной. Пределы интегрирования во внутреннем интеграле зависят от x, т.е. от переменной интегрирования во внешнем интеграле. Результат вычисления во внутреннем интеграле есть функция от x. Затем вычисляют внешний интеграл от полученной функции по переменной x. Пределы интегрирования во внешнем интеграле всегда постоянные величины, т.к. это наибольшее и наименьшее значения переменной x в области D. Замечания: 1. Пусть область
В этом случае во внутреннем интеграле переменная интегрирования – x, а y – величина фиксированная. Результат внутреннего интегрирования – функция от y, а в результате внешнего интегрирования её по y получим некоторое постоянное число; “c” и“d” – числа – наименьшее и наибольшее значение y на 2. Формулы (1) и (2) выведены в предположении, что область 3. Пусть область
Если область D - прямоугольник, то пределы внутреннего и внешнего интегрирования - константы (обратное справедливо). И если при этом функция Пример 1:Изменить порядок интегрирования в двойном интеграле:
|

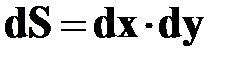 и
и . Предположим, что
. Предположим, что  . Тогда
. Тогда

 , и проведем через него плоскость // ZoY. Получаем S(x) – площадь поперечного сечения. Очевидно, что
, и проведем через него плоскость // ZoY. Получаем S(x) – площадь поперечного сечения. Очевидно, что , но S(x) =
, но S(x) = 

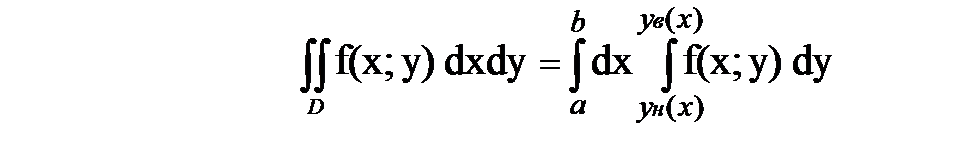 или в более удобном виде:
или в более удобном виде: имеет другой специальный вид:
имеет другой специальный вид: = =
= =  =
=  (2)
(2)


 разделяющаяся, т.е.
разделяющаяся, т.е.  ,то
,то 





