Известно, что двойной интеграл не зависит ни от способа разбиения области  на части, ни от выбора точки
на части, ни от выбора точки  . Рассмотрим область
. Рассмотрим область  в полярной системе координат. Пусть полюс совпадает с началом координат, ось Ox – с полярной осью.
в полярной системе координат. Пусть полюс совпадает с началом координат, ось Ox – с полярной осью.

 Разобьём область D на частичные области линиями
Разобьём область D на частичные области линиями
 и
и  , т.е. концентрическими окружностями и лучами, исходящими из полюса. Частичной областью
, т.е. концентрическими окружностями и лучами, исходящими из полюса. Частичной областью  будет криволинейный четырёхугольник.
будет криволинейный четырёхугольник.



Обозначим  (среднее),
(среднее),  .
.
В каждой площадке 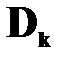 площадью
площадью  возьмём точку
возьмём точку  , лежащую на дуге
, лежащую на дуге  . Пусть
. Пусть  в декартовой системе координат соответствует
в декартовой системе координат соответствует 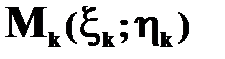

 ;
;  , тогда
, тогда 
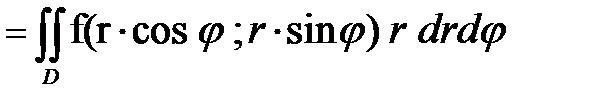 , т.е.
, т.е.
 (3)
(3)

 Рассмотрим задачу замены переменных в двойном интеграле по области D в общем случае. Предполагается, что функции
Рассмотрим задачу замены переменных в двойном интеграле по области D в общем случае. Предполагается, что функции  и
и  взаимно однозначны, непрерывны и имеют непрерывные частные производные на
взаимно однозначны, непрерывны и имеют непрерывные частные производные на  , т.е. установлено взаимно-однозначное соответствие между
, т.е. установлено взаимно-однозначное соответствие между  и
и 
Формула замены переменных для двойного интеграла для зависимостей
 и
и  имеет вид:
имеет вид:  , где
, где

– функциональный определитель  и
и  или Якобиан (нем. мат. Густав Якоб Якоби 1804-1851).
или Якобиан (нем. мат. Густав Якоб Якоби 1804-1851).
Пример (Лунгу № 3.2.2):
Сведение двойного интеграла в полярных координатах к повторному.
Пусть полюс точки O не принадлежит области D.
 Область D может быть заключена между двумя радиус-векторами,
Область D может быть заключена между двумя радиус-векторами,  и
и  .
.
Уравнение кривой ACB 
Уравнение кривой AFB 


 на части, ни от выбора точки
на части, ни от выбора точки  . Рассмотрим область
. Рассмотрим область 
 Разобьём область D на частичные области линиями
Разобьём область D на частичные области линиями и
и  , т.е. концентрическими окружностями и лучами, исходящими из полюса. Частичной областью
, т.е. концентрическими окружностями и лучами, исходящими из полюса. Частичной областью  будет криволинейный четырёхугольник.
будет криволинейный четырёхугольник.


 (среднее),
(среднее),  .
.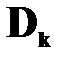 площадью
площадью  возьмём точку
возьмём точку  , лежащую на дуге
, лежащую на дуге  . Пусть
. Пусть  в декартовой системе координат соответствует
в декартовой системе координат соответствует 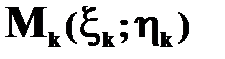

 ;
;  , тогда
, тогда 
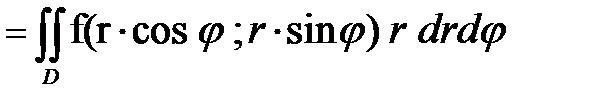 , т.е.
, т.е. (3)
(3)
 Рассмотрим задачу замены переменных в двойном интеграле по области D в общем случае. Предполагается, что функции
Рассмотрим задачу замены переменных в двойном интеграле по области D в общем случае. Предполагается, что функции  и
и  взаимно однозначны, непрерывны и имеют непрерывные частные производные на
взаимно однозначны, непрерывны и имеют непрерывные частные производные на  , т.е. установлено взаимно-однозначное соответствие между
, т.е. установлено взаимно-однозначное соответствие между  и
и 
 и
и  имеет вид:
имеет вид:  , где
, где
 и
и  или Якобиан (нем. мат. Густав Якоб Якоби 1804-1851).
или Якобиан (нем. мат. Густав Якоб Якоби 1804-1851). Область D может быть заключена между двумя радиус-векторами,
Область D может быть заключена между двумя радиус-векторами,  и
и  .
.





