Задача, приводящая к понятию двойного интеграла.P.S. Уважаемые соискатели, проверяйте Вашу анкету перед отправкой, пожалуйста! Внимательно проверяйте грамматические и пунктуационные ошибки, оформление, корректность предоставленных данных. Глава 14. Двойной интеграл Предварительные замечания. Def: Кривая называется простой, если её можно разбить на конечное число частей так, чтобы каждая из частей была записана уравнением, либо
Разобьём область D сетью простых линий на n – частей. Каждая часть Dk будет иметь площадь (т.к. по теореме она ограничена простой кривой). Def: Диаметр области Dk – наибольшее расстояние между двумя точками, принадлежащими области Dk (обозначим dk). Задача, приводящая к понятию двойного интеграла. Пусть функция Def: Тело, ограниченное плоскостью XOY, поверхностью Для вычисления объёма данного цилиндроида выполним следующие операции:
3. Для нахождения Vk выберем в области Dk произвольную точку @ 4.
|
, либо 
.
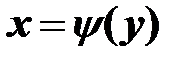Теорема: Если замкнутая область D на плоскости XOY ограничена простой кривой, то она имеет площадь.
- функция двух переменных, 
, где 
- это некоторая замкнутая область D, ограниченная простой кривой Г.
и с боков цилиндрической поверхностью, образующая которой // оси OZ, а направляющей служит контур Г, ограничивающий область D, называется цилиндроидом.
через@ Диаметры областей Dk, через -@
2. Построим на простых кривых разбиения области D цилиндроиды, тогда
@, где Vk – объём цилиндроида с основанием Dk.
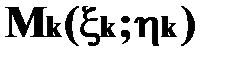, тогда,@ т.к. верхняя граница цилиндроида – поверхность произвольной формы, заменена участком плоскости параллельным xOy
