Полюс принадлежит области D.
В частном случае при
Замечание: В свойстве отмечалось, что если В полярной системе координат если Пример:
Приложение двойного интеграла к решению геометрических и физических задач. П.1 Вычисление площадей плоских фигур. При
п.2 Вычисление объёмов тел с помощью двойного интеграла. С геометрической точки зрения Пример: Вычислить V тела, ограниченного поверхностями: y=x2; y=1; x+y+z=4; z=0.
. П.3 Физический смысл двойного интеграла. Пусть D – плоская пластина, лежащая в плоскости x0y с поверхностной плотностью
Статические моменты пластины относительно осей 0x и 0y находят по формулам:
Координаты центра масс пластины: Моменты инерции пластины D относительно осей координат и начала координат:
|
Уравнение Г границы контура 
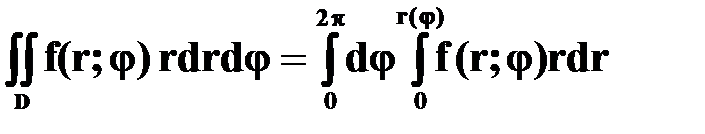
(т.е. область D – окружность с центром в полюсе)
, то двойной интеграл 
, т.е. площади D.
,то 
- формула площади в полярной системе координат.
, D: 
Перейдём в полярную систему координат:
; 
; 
- уравнение лемнискаты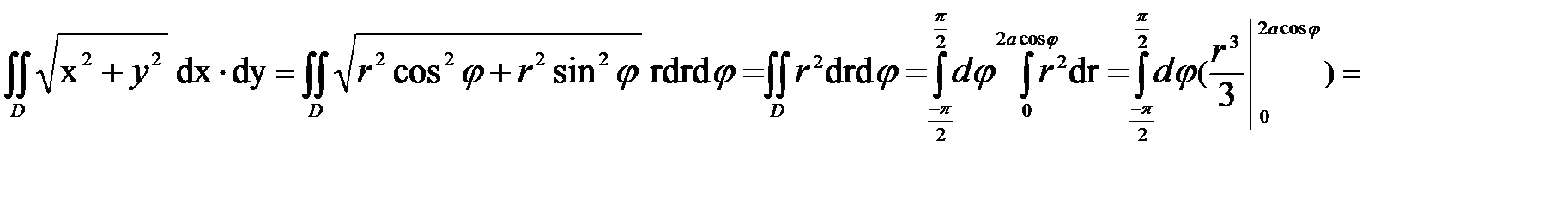
; 
Пример: Вычислить площадь фигуры, ограниченной линиями: xy=4; y=x; x=4.
(кв. ед).
,ограниченного сверху –f(x;y), снизу – областью D, с боков – некоторой цилиндрической поверхностью,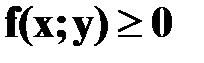 
. В цилиндрической системе координат: 
.
, тогда массу этой пластины можно найти по формуле:
; 
; 
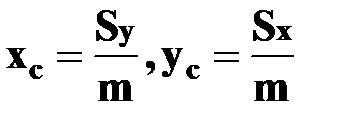
