Формулы Грина
Если бы в электростатических задачах мы всегда имели дело с дискретным или непрерывным распределением заряда без всяких граничных поверхностей, то общее решение для скалярного потенциала
было бы самой удобной и непосредственной формой решения таких задач и не нужны были бы ни уравнение Лапласа, ни уравнение Пуассона. Однако в действительности в целом ряде, если не в большинстве, задач электростатики мы имеем дело с конечными областями пространства (содержащими или не содержащими заряд), на граничных поверхностях которых заданы определённые граничные («краевые») условия. Эти граничные условия могут быть заменены некоторым соответственно подобранным распределением зарядов вне рассматриваемой области (в частности, в бесконечности), однако приведённое выше соотношение в этом случае уже непригодно для расчёта потенциала, за исключением некоторых частных случаев (например, в методе изображений). Для рассмотрения задач с граничными условиями необходимо расширить используемый нами математический аппарат, а именно вывести так называемые формулы, или теоремы Грина (1824 г.). Они получаются непосредственно из теоремы о дивергенции
которая справедлива для любого векторного поля А, определённого в объёме V, ограниченном замкнутой поверхностью S. Пусть
и
где
Напишем такую же формулу, поменяв в ней местами
В физике и математике теорема Грина дает соотношение между криволинейным интегралом простой ограниченной кривой С и двойным интегралом по плоской поверхности D ограниченной кривой С. И в общем виде записывается следующим образом
В физике Теорема Грина в основном используется для решения двумерных потоковых интегралов, исходя из того, что сумма исходящих потоков в любой точки области равна результирующему потоку, суммируемому по всей ограничивающей поверхности. Третье уравнение Грина получается из второго уравнения путем замены
|


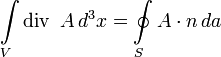 ,
, , где
, где  и
и  — произвольные дважды непрерывнодифференцируемые скалярные функции. Тогда
— произвольные дважды непрерывнодифференцируемые скалярные функции. Тогда
 ,
, — нормальная производная на поверхности S (по направлению внешней нормали по отношению к объёму V). Подставляя (1) и (2) в теорему о дивергенции, мы придем к первой формуле Грина
— нормальная производная на поверхности S (по направлению внешней нормали по отношению к объёму V). Подставляя (1) и (2) в теорему о дивергенции, мы придем к первой формуле Грина .
. сократятся и мы получим вторую формулу Грина, называемую иначе теоремой Грина:
сократятся и мы получим вторую формулу Грина, называемую иначе теоремой Грина: .
.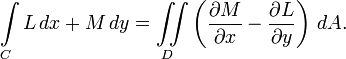
 и замечания о том, что
и замечания о том, что  в R ³. Если
в R ³. Если  дважды дифференцируема на U.
дважды дифференцируема на U.
 если x ∈ Int U,
если x ∈ Int U, 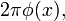 если x ∈ ∂ U и плоскость касания только в x.
если x ∈ ∂ U и плоскость касания только в x.


