Свойства криволинейного интеграла второго рода
Криволинейный интеграл II рода обладает следующими свойствами: 1. Пусть C обозначает кривую с началом в точке A и конечной точкой B. Обозначим через −C кривую противоположного направления - от B к A. Тогда
2. Если C − объединение кривых C 1 и C 2 (рисунок 2 выше), то
3. Если кривая C задана параметрически в виде
4. Если кривая C лежит в плоскости O xy и задана уравнением
21 Формула Грина Теорема Грина устанавливает связь между криволинейным интегралом по замкнутому контуру Формулировка Пусть
На символе интеграла часто рисуют окружность, чтобы подчеркнуть, что кривая [править] Доказательство
Пусть область
Для кривой Тогда:
Заметим, что оба полученных интеграла можно заменить криволинейными интегралами:
Интеграл по Криволинейные интегралы по
Заменим в (1) интегралы согласно (2) и (3), а также прибавим (4) и (5), равные нулю и поэтому не влияющие на значение выражения:
Так как обход по часовой стрелке при правой ориентации плоскости является отрицательным направлением, то сумма интегралов в правой части является криволинейным интегралом по замкнутой кривой
Аналогично доказывается формула:
если в качестве области Складывая (6) и (7), получим:
|



 , то
, то
 (предполагается, что R = 0и t = x), то последняя формула записывается в виде
(предполагается, что R = 0и t = x), то последняя формула записывается в виде
 и двойным интегралом по области
и двойным интегралом по области  , ограниченной этим контуром. Фактически, эта теорема является частным случаем более общей теоремы Стокса. Теорема названа в честь английского математика Джорджа Грина.
, ограниченной этим контуром. Фактически, эта теорема является частным случаем более общей теоремы Стокса. Теорема названа в честь английского математика Джорджа Грина. ,
,  определены в области
определены в области  ,
,  , то
, то


 , ограниченная замкнутой кривой
, ограниченная замкнутой кривой 


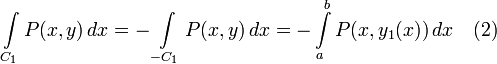

 берётся со знаком «минус», так как согласно ориентации контура
берётся со знаком «минус», так как согласно ориентации контура  до
до  .
. и
и  будут равны нулю, так как
будут равны нулю, так как  :
:




 .
.



