Го рода
Определение Пусть кривая C описывается векторной функцией Если на кривой C определена скалярная функция F, то интеграл
Криволинейный интеграл
Свойства криволинейного интеграла первого рода Криволинейный интеграл I рода обладает следующими свойствами: 1. Интеграл не зависит от ориентации кривой;
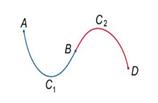
2. Пусть кривая C 1 начинается в точке A и заканчивается в точке B, а кривая C 2 начинается в точке B и заканчивается в точке D (рисунок 2). Тогда их объединением будет называться кривая C 1 U C 2, которая проходит от A к B вдоль кривой C 1 и затем от B к D вдоль кривой C 2. Для криволинейных интегралов первого рода справедливо соотношение
3. Если гладкая кривая C задана параметрически соотношением
4. Если C является гладкой кривой в плоскости O xy, заданной уравнением
5. Если гладкая кривая C в плоскости O xy определена уравнением
6. В полярных координатах интеграл
где кривая C задана в полярных координатах функцией Го рода
|
, где переменная s представляет собой длину дуги кривой (рисунок 1).
называется криволинейным интегралом первого рода от скалярной функции F вдоль кривой C и обозначается как
существует, если функция F непрерывна на кривой C.
и скалярная функция F непрерывна на кривой C, то
, то
, то
выражается формулой
.
