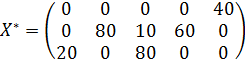транспортного типа.
Дано: с трех складов А1, А2, А3 необходимо доставить овощи в пять торговых точек В1, В2, В3, В4, В5. Требуется закрепить склады за торговыми точками так, чтобы общая сумма затрат на перевозку была минимальной. Числовые данные представлены в следующей таблице:
Найти: оптимальный план доставки продукции, при котором совокупные транспортные затраты будут минимальными. Решение: Обозначим искомые объемы поставок от i -й базы–поставщика к j -му заводу-потребителю через xij Суммарные затраты на перевозку грузов составят:
Мощности всех складов (баз-поставщиков) должны быть реализованы, спрос заводов-потребителей – удовлетворен, т.е.:
I итерация. 1 этап: проверка сбалансированности запасов и потребностей. Определим суммарную мощность баз-поставщиков:
Определим суммарную мощность заводов-потребителей:
Поскольку транспортная задача закрытая, т.е.
значит она в настоящем виде имеет решение. 2 этап: разработка исходного опорного плана (методом минимальной стоимости) В исходной таблице наименьшей стоимостью транспортировки обладает ячейка (2-4), равная единице. Данную ячейку будем заполнять в первую очередь. Объем поставок (т.е. цифра, которая будет занесена в ячейку (2-4)) определяется по формуле:
Запишем в ячейку (2-4) объем поставок
Записав 60 в ячейку (2-4), мы полностью удовлетворили спрос завода-потребителя В4, поэтому в столбце В4 в ячейках (1-4) и (3-4) рисуем косые черты. Данные ячейки в разработке исходного опорного плана не принимают участия. В полученной таблице наименьшей стоимостью транспортировки обладают ячейки (1-5), (2-2), (3-3). Определим объем поставок, которые можно будет записать в каждую из этих ячеек:
Из данных трех ячеек будем в первую очередь выбирать ту, которую можно загрузить большим значением, т.е. Записав значение 90 в ячейку (3-3), мы полностью удовлетворили спрос завода-потребителя В3, поэтому в ячейках (1-3) и (2-3) рисуем косые черты. В полученной таблице наименьшей стоимостью транспортировки обладают ячейки (1-5) и (2-2). Выбираем ячейку (2-2), поскольку потребности завода-потребителя В2 больше, чем у В5.
В полученной таблице наименьшей стоимостью транспортировки обладает ячейка (1-5).
Записав значение 40 в ячейку (1-5), мы: а) полностью удовлетворили спрос завода-потребителя В5, поэтому в ячейки (2-5) и (3-5) ставим косые черты; б) полностью использовали запасы базы-поставщика А1, поэтому в ячейку (1-1) также ставим косую черту. Из полученной таблицы видно, что спрос завода-потребителя В1 в 20 ед. товара будет удовлетворен базой-поставщиком А2 на 10 ед., базой-поставщиком А3 – на 10 ед. Внеся данные значения (т.е. по 10 ед. в ячейки (2-1) и (3-1)), получим следующую таблицу:
Совокупные транспортные затраты для данного плана поставок составят:
3 этап: проверка вырожденности опорного плана Для дальнейшего решения транспортной задачи необходимо, чтобы опорный план был невырожденным, т.е. число заполненных (задействованных) клеток в таблице равнялось
m – число баз-поставщиков; n – число заводов-потребителей. Поскольку В качестве фиктивной ячейки мы возьмем ячейку (1-2), поскольку среди незаполненных ячеек ее стоимость минимальна (равна 3) и на основе этой ячейки невозможно построить замкнутый цикл со всеми заполненными ячейками. Введя фиктивную ячейку, мы построим невырожденный опорный план, т.е.
4 этап: расчет потенциалов баз-поставщиков Расчет потенциалов выполняют по загруженным (заполненным) ячейкам таблицы поставок, для которых:
Пусть
Занесем результаты расчетов в таблицу поставок:
5 этап: проверка плана на оптимальность По полученной таблице для незагруженных (незаполненных) ячеек проверим условие оптимальности:
Опорный план не оптимальный, т.к. имеются ячейки 6 этап: поиск «вершины максимальной неоптимальности» (ВМН) Поиск осуществляется по незагруженным ячейкам, для которых условие оптимальности не соблюдается по формуле:
Среди полученных оценок находят наибольшую, т.е.
7 этап: построение контура перераспределения поставок
8 этап: определение минимального элемента в контуре перераспределения поставок и осуществление перераспределения поставок по контуру. Среди ячеек со знаком «–» выбираем ту, у которой значение объема поставок меньше:
Из ячеек со знаком «–» отнимаем из значения объема поставок по 10, а в ячейки со знаком «+» - прибавляем по 10. 9 этап: получение нового опорного плана.
Совокупные транспортные затраты для данного плана поставок составят:
II итерация. 3 этап: проверка вырожденности опорного плана Поскольку 4 этап: расчет потенциалов баз-поставщиков Пусть
Занесем результаты расчетов в таблицу поставок:
5 этап: проверка плана на оптимальность
Поскольку для всех незагруженных (незаполненных) ячеек соблюдается условие:
Поскольку ни для одной незаполненной ячейки не выполняется условие Ответ: оптимальное распределение поставок
Данное распределение поставок обеспечит оптимальные транспортные затраты в размере 550 условных денежных единиц.
|

 Заводы- потребители
Заводы- потребители



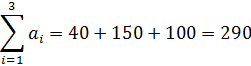



 .
.



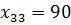 .
.



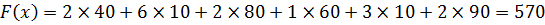
 , где:
, где: (т.е. не выполняется условие
(т.е. не выполняется условие  ), следовательно опорный план вырожденный и его необходимо сделать невырожденным путем введения дополнительной заполненной нулем ячейки (т.е. фиктивной ячейки).
), следовательно опорный план вырожденный и его необходимо сделать невырожденным путем введения дополнительной заполненной нулем ячейки (т.е. фиктивной ячейки).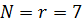

 и заводов-потребителей
и заводов-потребителей 
 , где
, где - потенциал i -й строки;
- потенциал i -й строки; - потенциал j -го столбца;
- потенциал j -го столбца;








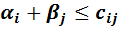


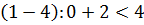

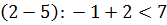



 и
и  , для которых условие оптимальности не выполняется.
, для которых условие оптимальности не выполняется.

 соответствует ВМН, в данную ячейку ставят знак «+».
соответствует ВМН, в данную ячейку ставят знак «+».






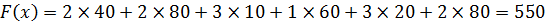











 ,следовательно, оптимальный опорный план является единственным.
,следовательно, оптимальный опорный план является единственным.