Введение поправок. Неисключенная систематическая погрешность

Систематические погрешности являются детерминированными величинами, поэтому в принципе всегда могут быть вычислены и исключены из результатов измерений. После исключения систематических погрешностей получаем исправленные средние арифметические и исправленные отклонения результатов наблюдении, которые позволяют оценить степень рассеивания результатов.

Для исправления результатов наблюдений их складывают с поправками, равными систематическим погрешностям по величине и обратными им по знаку. Поправку определяют экспериментально при поверке приборов или в результате специальных исследований, обыкновенно с некоторой ограниченной точностью. Для исправления результата наблюдения его складывают только со средним арифметическим значением поправки:

,

(59)

где и – соответственно исправленный и неисправленный результаты наблюдений, – среднее арифметическое значение поправки, определяемые экспериментально.

Поправки могут задаваться также в виде формул, по которым они вычисляются для каждого конкретного случая. Например, при измерениях и поверках с помощью образцовых манометров следует вводить поправки к их показаниям на местное значение ускорения свободного падения

,

где – измеряемое давление.

Введением поправки устраняется влияние только одной вполне определенной систематической погрешности, поэтому в результаты измерения зачастую приходится вводить очень большое число поправок. При этом вследствие ограниченной точности определения поправок накапливаются случайные погрешности и дисперсия результата измерения увеличивается.

Действительно, при исправлении неисправленного результата путем введения поправок по формуле

,

(60)

дисперсия становится равной

,

(61)

где – оценка дисперсии неисправленных результатов; – оценка дисперсии -й поправки.

Поправку имеет смысл вводить до тех пор, пока она уменьшает доверительные границы погрешности, т.е. пока выполняется неравенство

.

(62)

При малой дисперсии поправки на основании формулы (62) может показаться, что введение любой поправки повышает достоверность результата. Однако следует помнить, что погрешность результата выражается не более чем двумя значащими цифрами, поэтому поправка, если она меньше пяти единиц разряда, следующего за последним десятичным знаком погрешности результата, будет все равно потеряна при округлении, и вводить ее не имеет смысла.

Систематическая погрешность, остающаяся после введения поправок на ее наиболее существенные составляющие включает в себя ряд элементарных составляющих, называемых неисключенными остатками систематической погрешности. К их числу относятся:

• погрешности определения поправок;
• погрешности, зависящие от точности измерения влияющих величин, входящих в формулы для определения поправок;
• погрешности, связанные с колебаниями влияющих величин (температуры окружающей среды, напряжения питания и т.д.).

Перечисленные погрешности малы и поправки на них не вводятся.

Для каждого данного измерения элементарные составляющие систематической погрешности имеют вполне определенные значения, но эти значения нам неизвестны. Известно лишь, что в массе однотипных измерений эти составляющие лежат в определенных границах 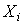или имеют определенные средние квадратические отклонения . В первом случае для неисключенных остатков следует принять равномерное распределение, во втором – нормальное. Дисперсия суммы неисключенных остатков систематической погрешности определяется как сумма их дисперсий и поэтому

,

(63)

где m₁ – число равномерно распределенных и m₂ – число нормально распределенных элементарных составляющих.