Способы измерения влияния факторов в стохастическом анализе
Наиболее распространенным способом является корреляционный анализ. Корреляционной связью называется такая стохастическая связь, при которой различным значениям одной переменной соответствуют разные средние значения другой. При проведении корреляционного анализа строят различные корреляционные модели хозяйственной деятельности. В зависимости от количества исследуемых показателей различают парные и многофакторные модели корреляционного анализа. Парная корреляция – это связь между двумя показателями, один из которых является факторным, а другой – результативным. Множественная корреляция возникает от взаимодействия нескольких факторов с результативным показателем. Условия применения корреляционного анализа: 1. наличие достаточно большого количества наблюдений о величине исследуемых факторных и результативных показателей 2. исследуемые факторы должны иметь количественное измерение и отражение в тех или иных источниках информации. Основной задачей корреляционного анализа является выявление формы и тесноты связи между результативным и факторным показателями. Под формой связи понимается тип аналитической формулы, выражающей зависимость результативного показателя от изменений факторного. Различают связь прямую, когда с ростом (снижением) значений факторного показателя наблюдается тенденция к росту (снижению) значений результативного показателя. В противном случае между показателями существует обратная связь. Форма связи может быть прямолинейной (ей соответствует уравнение прямой линии), когда наблюдается тенденция равномерного возрастания или убывания результативного показателя, в противном случае форма связи называется криволинейной (ей соответствует уравнение параболы, гиперболы и др.). Практическая реализация корреляционного анализа включает следующие этапы: 1) постановка задачи и отбор факторов, оказывающих воздействие на изучаемый показатель Необходимо отбирать самые значимые факторы, которые оказывают наиболее существенное воздействие на результативный показатель. Не рекомендуется включать в корреляционную модель взаимосвязанные факторы, иначе это приведет к искажению результатов анализа. 2) сбор информации и ее первичная обработка (группировки, исключение аномальных наблюдений, проверка нормальности распределения) Информация должна быть проверена на точность, однородность и соответствие закону нормального распределения. Если в совокупности имеются группы объектов, которые значительно отличаются от среднего уровня, то это говорит о неоднородности исходной информации. Критериями однородности информации служат среднеквадратическое отклонение и коэффициент вариации, которые рассчитываются по каждому факторному и результативному показателю. Среднеквадратическое отклонение (σ; [сигма]) показывает абсолютное отклонение индивидуальных значений от средней арифметической; оно рассчитывается по формуле:
Коэффициент вариации (υ; [ипсилон]) показывает относительную меру отклонения отдельных значений от средней арифметической, он рассчитывается так:
где
n – количество наблюдений в совокупности. Чем больше коэффициент вариации, тем относительно больший разброс и меньшая выравненность изучаемых объектов, что свидетельствует о неоднородности информации и о необходимости исключения нетипичных наблюдений. 3) моделирование связей между факторами и результативными показателями На этом этапе подбирается и обосновывается математическое уравнение, которое наиболее точно выражает сущность исследуемой зависимости. При прямолинейной зависимости парная регрессия будет иметь вид:
а множественная регрессия:
а – постоянная величина результативного показателя, которая не связана с изменением факторов; в1, в2, … - коэффициенты регрессии (показывают среднее изменение результативного показателя с повышением или понижением величины факторного показателя на единицу его измерения) х1, х2, … - факторы. Примеры: парная корреляция – зависимость производительности труда от его фондовооруженности: множественная корреляция: зависимость рентабельности продаж от материалоотдачи (руб.), фондоотдачи (коп.), производительности труда (тыс.руб.), продолжительности оборота оборотных средств предприятия (дни), удельного веса продукции высшей категории качества (%):
4) расчет основных показателей связи корреляционного анализа: уравнение связи, коэффициенты корреляции, детерминации и др. Расчет уравнения связи сводится к определению параметров а и в. Их находят из системы уравнений:
Таким образом, можно определить степень связей между показателями. Для изучения тесноты связи между факторными и результативным показателями определяется коэффициент корреляции, детерминации. В анализе хозяйственной деятельности чаще используется линейный коэффициент парной корреляции (ρ; [ро]). Он определяется по формуле:
Значение коэффициента парной корреляции изменяется в интервале [-1; + 1]. Знак «+» означает наличие прямой связи между показателями, знак «-» - обратной. Значение коэффициента от 0 до 1 характеризует степень приближения корреляционной зависимости между показателями к функциональной. Если линейной связи между факторами не наблюдается, ρ = 0.
5) статистическая оценка и практическое использование результатов корреляционного анализа Чтобы убедиться в надежности показателей связи и правомерности их использования для практических целей, необходимо дать им статистическую оценку. В результате выявляется, может ли быть использовано уравнение для практических целей, а именно для расчета влияния факторов на прирост результативного показателя; подсчета резервов повышения уровня исследуемого показателя и планирования и прогнозирования его величины. Влияние каждого фактора на результативный показатель рассчитывается следующим образом:
Расчет резервов роста результативного показателя:
Многофакторный корреляционный анализ имеет важную научную и практическую значимость. С установлением места и роли каждого фактора в формировании уровня исследуемых показателей точнее обосновываются планы и управленческие решения, объективнее оцениваются итоги деятельности предприятий, и полнее определяются внутрихозяйственные резервы. Кластерный анализ - один из методов многомерного анализа, предназначенный для группировки (кластеризации) совокупности, элементы которой характеризуются многими признаками. Значения каждого из признаков служат координатами каждой единицы изучаемой совокупности в многомерном пространстве признаков. Каждое наблюдение, характеризующееся значениями нескольких показателей, можно представить как точку в пространстве этих показателей, значения которых рассматриваются как координаты в многомерном пространстве. Основным критерием кластеризации является то, что различия между кластерами должны быть более существенны, чем между наблюдениями, отнесенными к одному кластеру. Дисперсионный анализ - это статистический метод, позволяющий определить, к одной и той же совокупности данных или нет относятся группы разных наблюдений. Он часто используется совместно с методами группировки. Задача его проведения в этих случаях состоит в оценке существенности различий между группами. Для этого определяют групповые дисперсии σ12 и σ;22, а затем по статистическим критериям Стьюдента или Фишера проверяют значимость различий между группами.
|

 ;
; 
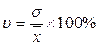
 - значения факторного и результативного показателей соответственно;
- значения факторного и результативного показателей соответственно; - средние значения соответствующих показателей;
- средние значения соответствующих показателей;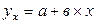

 .
.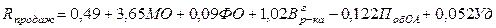
 , п – число наблюдений
, п – число наблюдений
 .
.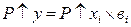
 - резерв роста.
- резерв роста.


