Пространственное распределение амплитуды лазерного излучения. Розрахунок основної заробітної плати меліораторів П.І.Б. Площа обробки, га Розцінки грн./га Заробітна плата
Розрахунок основної заробітної плати меліораторів
Теоретическая часть Пространственное распределение амплитуды лазерного излучения Для того чтобы правильно описать излучение, преобразованное линзой или сложной оптической системой, прежде всего, необходимо знать, что представляет собой само лазерное изучение. Следует четко помнить, что параметры лазерного излучения полностью определяются конфигурацией резонатора лазера, то есть радиусами кривизны резонатора R 1 и R 2 и расстоянием L между ними. Нахождение лазерного излучения от резонатора с известной конфигурацией основано на скалярной теории дифракции монохроматического излучения. Применение принципа Гюйгенса - Френеля при условии существенной кривизны волновых фронтов (радиусы их кривизны значительно больше длины волны излучения) и малости дифракционных углов позволяет описать результат дифракции с помощью интеграла Френеля-Кирхгофа (1).
где E (ξ, η,0) - поле на элементе, на котором происходит дифракция излучения. (см. рис.1)

Нас интересуют стационарные распределения оптического поля в резонаторе лазера, то есть распространение излучения с амплитудой E от поверхности одного зеркала резонатора к другому и обратно. Таким образом распределение поля на зеркалах νр (x, y) в стационарном режиме остается неизменным. Задаваясь некоторым исходным распределением νр (ξ, η) и описывая с помощью (1) достаточно большое количество последовательных переотражений, при определенных условиях может быть достигнута практическая неизменность (стационарность) амплитуды излучения в резонаторе, которая и соответствует искомой функции
Каждый из этих пучков наиболее просто описывается через функции
где Зависимости
Из (3) следует, что кривизна волнового фронта гауссового пучка
с радиусом кривизны
ассимптоты которого определяют угол расходимости гауссового пучка
Из выражений (3) и (4) следует, что величина радиуса кривизны волнового фронта R (z) и радиуса пятна в сечении перетяжки не зависят от модовых чисел m и n, т.е. одинаковы для всех мод эрмито-гауссового пучка. Поэтому анализ лазерного излучения и его преобразование оптической системой целесообразно проводить только для основной моды (ТЕМ00) с нулевым значением модовых чисел. При этом выражение (2) описывает чисто гауссов пучок, для которого изменение амплитуды в поперечном сечении представляет собой гауссоиду
Постоянная v0 в выражениях (2) и (5) связана с энергетическими характеристиками лазерного пучка: с его интенсивностью
и потенциалом
После интегрирования из последнего выражения следует:
В результате пространственное распределение интенсивности излучения лазера можно записать в виде, удобном для практических расчетов:
Таким образом, все основные зависимости, описывающие пространственное распределение лазерного излучения, в конечном счете, выражаются через радиус перетяжки r0 и параметр конфокальности zK. Последние в свою очередь определяются конфигурацией резонатора.
|

 (1)
(1) . Этот метод последовательных приближений при ряде допущений позволяет получить аналитическое решение для лазера с устойчивым резонатором, излучение которое представляет собой набор эрмитогауссовых пучков.
. Этот метод последовательных приближений при ряде допущений позволяет получить аналитическое решение для лазера с устойчивым резонатором, излучение которое представляет собой набор эрмитогауссовых пучков.
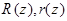 и параметры
и параметры  , характеризующие геометрию гауссова пучка, и определяется выражением (2), (3):
, характеризующие геометрию гауссова пучка, и определяется выражением (2), (3): (2)
(2) - полиномы Чебышева - Эрмита, k = 0, 1, 2, 3, …; например,
- полиномы Чебышева - Эрмита, k = 0, 1, 2, 3, …; например, 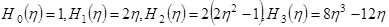 и т.д. n, m - модовые числа;
и т.д. n, m - модовые числа;  - радиус кривизны волнового фронта в точке (0, 0, z);
- радиус кривизны волнового фронта в точке (0, 0, z);  - радиус пятна по уровню амплитуды 1/e в плоскости, пересекающей ось OZ в точке (0, 0, z) и перпендикулярной этой оси;
- радиус пятна по уровню амплитуды 1/e в плоскости, пересекающей ось OZ в точке (0, 0, z) и перпендикулярной этой оси;  - радиус пятна в сечении перетяжки;
- радиус пятна в сечении перетяжки;  - параметр конфокальности пучка.
- параметр конфокальности пучка. и
и  в выражении (2) имеют вид
в выражении (2) имеют вид (3)
(3) изменяется от максимального (в сечениях
изменяется от максимального (в сечениях  ) до минимального (нулевого) значения при
) до минимального (нулевого) значения при  и
и  . Как может быть показано [4], фазовая поверхность представляет собой параболоид вращения:
. Как может быть показано [4], фазовая поверхность представляет собой параболоид вращения:
 для точки на оси (0, 0, z), который определяется зависимостью (3). В то время как огибающая гауссового пучка по уровню амплитуды 1/ e есть гиперболоид вращения (см. рис. 2)
для точки на оси (0, 0, z), который определяется зависимостью (3). В то время как огибающая гауссового пучка по уровню амплитуды 1/ e есть гиперболоид вращения (см. рис. 2)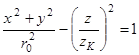 ,
, (4)
(4)
 (5)
(5)


 (6)
(6)


