Ознакомиться с теоретической частью работы и подготовить ответы на контрольные вопросы.
1 часть. Измерение параметров преобразованного гауссова пучка интерференционным методом.
1. Рассчитать параметры z01, z K1, 2θ 1 гауссова пучка, формируемого лазером ЛГН-208А, и пучка, преобразованного оптической системой (расстояние b 2 между лазером и объективом задается преподавателем).
2. На лабораторной установке (рис. 7) для преобразованного гауссова пучка провести измерения величин α 1, Δ x k(α 1), α 2, Δ x k(α 2) (при выбранном k) и расстояние Δ z.
3. Рассчитать экспериментальные значения параметров r Э01, z ЭK1, 2θ Э1 для преобразованного пучка. Провести сравнение теоретических и экспериментальных значений параметров.
2 часть. Измерение параметров гауссова пучка, формируемого лазером, энергетическим методом.
1. Рассчитать параметры z 02, z K2, 2θ 2 гауссова пучка для лазера ЛГН-208A.
2. На лабораторной установке (рис. 8) провести измерение величин P, P S(z 1), P S(z 2), z 12.
3. Рассчитать экспериментальные значения параметров r Э02, z ЭK2, 2θ Э2, и сравнить их с теоретическими значениями. Оформить отчет по лабораторной работе, который должен содержать основание содержания теоретической части, используемые в расчетах формульные зависимости, схемы лабораторных установок и результаты экспериментов, расчеты, проведенные при нахождении теоретических и экспериментальных параметров гауссовых пучков.
Контрольные вопросы
- В чем заключается метод последовательных приближений, используемый при нахождении поля устойчивого резонатора. Решением какого интегрального уравнения является выражение (3)?
- Как используется матричная оптика для анализа гауссовых пучков?
- Каким образом обосновывается возможность применения, и как используются методы геометрической оптики для анализа преобразования гауссовых пучков оптической системы? Какую форму для гауссова пучка имеют лучи в их классическом определении?
- По известному распределению энергии в сечении пучка и положению этого сечения относительно фокальных и главных плоскостей оптической системы построить распределение энергии в оптически сопряженном сечении.
- По известным форме огибающей гауссова пучка и положениям главных и фокальных плоскостей оптической системы найти графически расходимость пучка, преобразованного этой системой. Как может быть найдено сечение перетяжки преобразованного пучка?
- На каких свойствах гауссовых пучков основаны описанные методы измерений его параметров?
- Решением каких систем уравнений являются выражения (19') и (21), используемые при расчете параметров пучков по результатам измерений?
- При применении диафрагмы с круглым отверстием в энергетическом методе существенно упрощается обработка результатов. Почему диафрагма такой формы не использована в установке? Как изменится расчет, если щелевую диафрагму заменить на непрозрачную полосу, дополнительную к щели?
- Какие допущения приняты при теоретическом описании результата интерференции смещенных гауссовых пучков?
- Какие погрешности в лабораторных установках наиболее существенно влияют на точность экспериментально определяемых параметров.
*) Вопросы 3, 8. и 10 для «отличников».
Приложения
Таблица 1
|
| Оптическая схема
| Матрица преобразования
|
| Перемещение в свободном пространстве
| 
| 
|
| Преломление на одной поверхности
|  
| 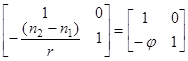
|
| Отражение от одной поверхности
| 
| 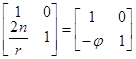
|
| Тонкая линза в воздухе с фокусным расстоянием
| 
| 
|
 Преобразование луча между двумя главными плоскими системами линз в воздухе Преобразование луча между двумя главными плоскими системами линз в воздухе
|
| 
|
 Преобразование луча между фокальными плоскостями системы линз в воздухе Преобразование луча между фокальными плоскостями системы линз в воздухе
|
| 
|
 Преобразование луча между двумя сопряженными плоскостями поперечное увеличение Преобразование луча между двумя сопряженными плоскостями поперечное увеличение
|
| 
|
 Афокальная система с поперечным увеличением Афокальная система с поперечным увеличением
|
| 
|
Таблица 2
Таблица формул для расчета параметров лазерного излучения
| Неустойчивые резонаторы
| Рассматриваемое свойство
| Устойчивые резонаторы
|
| Условия резонатора
| След матрицы
A + D
| Условие резонатора
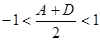
|


| положительная ветвь
отрицательная ветвь
|
 где где  *; *; 
| Главное собственное значение l/t берется положительным, а q в интервале [0, p]
|  ;
где ;
где  ; ;

|
Радиус кривизны

| Отношение компонент собственного вектора
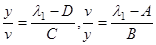
| Комплексный параметр кривизны

|
|
| Параметры гауссова пучка
|
|
|
| 1. Радиус кривизны
| 
| Измеряется в выходной плоскости
|
|
| 2. Расходимость волнового фронта
| 
|
|
| 3. Радиус сечения пучка
| 
|
|
| 4. Положение перетяжки
| 
|
|
| 5. Радиус в сечении перетяжки пучка
| 
|
|
| 6. Конфокальный параметр пучка
| 
|
|
| 7. Половина угла расходимости в дальней зоне (в радианах)
| 
|
| Хорошая при условии, что число Френеля системы достаточно велико
| Селекция мод
| Проявляется лишь при малых числах Френеля
|
| | | | | |
Литература
- Борн М., Вольф Э. Основы оптики: перевод с англ. /Пер. Г.Н. Мотулевич. -М.:Наука, 1973. -850с.
- Ананьев Ю.А. Неустойчивые резонаторы и их применение. - В кн. Квантовая электроника /Под ред. Н.Г. Басова. -М.:Сов. радио, 1971, №6, с.89-97.
- Ищенко Е.Ф., Климов Ю.М. Оптические квантовые генераторы. М.: Сов. радио, 1968. -468с.
- Пахомов И.И., Рожков О.В., Рождествин В.Н. Оптико-электронные квантовые приборы: учебное пособие для вузов /Под ред. И.И. Пахомова. -М.:Радио и связь, 1982. -456с.
- Джеррад А., Берч Дж.М. Введение в матричную оптику: пер. с англ. /Под ред. В.В. Коробкина. -М.:Мир, 1979. -540с.
- Пахомов И.И. Расчет преобразования лазерного пучка в оптических системах: учебное пособие по курсу "Физические основы оптикоэлектронных квантовых приборов" /Под ред. Л.Н. Лазарева. -М.:МВТУ им. Н.Э. Баумана. 1983. -54с.
- Мосягин Г.М., Немтинов В.Б. Теория преобразования сигналов в оптико-электронных приборах. М.:МВТУ. I, II. 1997.
- Справочник по специальным функциям /Под ред. М. Абрамовица и И. Стиган. -М.:Наука. 1979. -830с. (с.122-132).
Описание составил:
д.т.н., профессор И.И. Пахомов
Московский Государственный Технический Университет имени Н.Э.Баумана
Кафедра РЛ-2
"УТВЕРЖДАЮ"
ЗАВ. КАФЕДРОЙ РЛ-2
________________КОЗИНЦЕВ В.И.
" "_________________2003г.
Лабораторная работа
ПРЕОБРАЗОВАНИЕ ГАУССОВА ПУЧКА ОПТИЧЕСКОЙ СИСТЕМОЙ И ИЗМЕРЕНИЕ ЕГО ПАРАМЕТРОВ
Москва - 2003г.
* Там, где в формулах имеется два знака, верхний знак соответствует положительной ветви, а нижний - отрицательной.
ИЗУЧЕНИЕ ТЕХНОЛОГИИ МАКАРОННЫХ ИЗДЕЛИЙ
Цель: освоить технологию макаронных изделий на оборудовании мини-пекарни, расчет расхода сырья и методы анализа качества готового продукта





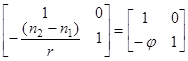

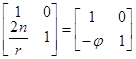


 Преобразование луча между двумя главными плоскими системами линз в воздухе
Преобразование луча между двумя главными плоскими системами линз в воздухе

 Преобразование луча между фокальными плоскостями системы линз в воздухе
Преобразование луча между фокальными плоскостями системы линз в воздухе

 Преобразование луча между двумя сопряженными плоскостями поперечное увеличение
Преобразование луча между двумя сопряженными плоскостями поперечное увеличение

 Афокальная система с поперечным увеличением
Афокальная система с поперечным увеличением

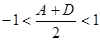


 где
где  *;
*; 
 ;
где
;
где  ;
;