Решение.
Таблица №1(Статистика
Таблица №2 (Значение
Таблица №3 (Значение коэффициента распределение Стьюдента с
Лабораторная работа №2. Биномиальное распределение.
Лабораторная работа выполняется в Excel 2007. Цель работы – дать навыки построения биномиального закона распределения и вычисления числовых характеристик средствами Excel.
Если вероятность наступления события в схеме испытаний Бернулли равно p, то вероятность того, что, что при n испытаниях событие появится ровно m раз, определяется формулой Бернулли:
Закон распределения случайной величины X, которая может принять n + 1 значение (0, 1, 2, …, n), описываемый формулой Бернулли, называется биномиальным. Задание. В серии одинаковых, независимых n испытаний вероятность успеха равна p. Построить ряд распределения, многоугольник и функцию распределения случайной величины x числа успехов. Найти математическое ожидание, дисперсию, среднее квадратическое отклонение. Пусть задано n = 7, p = 0,43
Найти вероятность: - трех успехов - хотя бы одного успеха - хотя бы одного успеха - не более четырех успехов - от двух до пяти успехов
Решение. 1. Построение ряда распределения случайной величины x – числа успехов в серии n испытаний.
Введите метки ячеек A1 – n (число испытаний); B1 – p (вероятность успеха); C1 – q (q = 1- p, вероятность неудачи).
Заполните ячейки A2, B2, C2 (соответственно n = 7, p = 0,43, q= 1 – p) как показано на рис. 1, используя при этом абсолютную адресацию (в ячейку B2 введите формулу = 0,43, а в ячейку C2 введите формулу =1 – $B$2). Введите метки ячеек A4 – x (число успехов) B4 – p (вероятность успеха); C4 – F(x) (функция распределения).
Рис. 1. Исходные данные
Массив A5:A12 содержит значения случайной величины x (число успехов).
В ячейку B5 занесите формулу биномиального распределения
используя функцию Excel ФАКТР (В Главном меню Excel → Формулы → Вставить функцию → Мастер функций – шаг 1 из 2 →категория Математические → ФАКТР → ОК).
Рис. 2. Строка формул с введенной формулой В результате вычислений в ячейке B5 появится значение вероятности p = 019549 события x = 0, рис.3.
Рис. 3. В ячейке B5 – вероятности p = 019549 появления случайной величины x = 0 для биномиального распределения Размножьте результат вычислений вероятности p в ячейки B6:B12.
Полученный таким образом ряд распределения показан на рис. 4 (ячейки B5:B12).
Построение многоугольника распределения. Выделите оба столбца исходных данных (A4:A12, B4:B12) вместе с метками x и p. В главном меню выберите закладку Вставка → График → Все типы диаграмм…→Точечная, и далее – график с точками, соединенными прямыми линиями. ОК.
Полученный график отформатируйте, как показано на рис.4.
Рис. 4. Ряд распределения (ячейки B5:B12) и многоугольник распределения
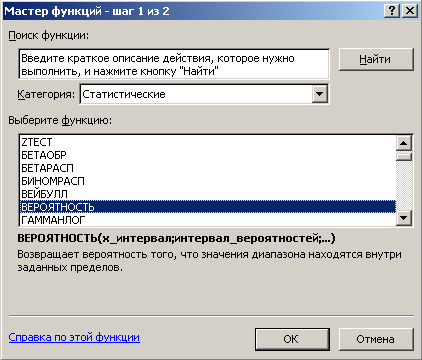
3. Построение функции распределения. Выделите ячейку C5. В главном меню Excel выберите закладку Формулы → Вставить функцию →;в диалоговом окне Мастер функций – шаг 1 из 2 в категории Статистические → ВЕРОЯТНОСТЬ. ОК.
Рис. 5. Диалоговое окно для выбора функции ВЕРОЯТНОСТЬ. В открывшемся диалоговом окне Аргументы функции ВЕРОЯТНОСТЬ заполните поля ввода как показано на рис. 6: X_интервал – $A$5: $A$12, столбец адресов ячеек переменной x; Интервал_вероятностей - $B$5: $B$12, столбец адресов ячеек переменной p; Нижний_предел - $A$5, адрес ячейки переменной x1;
|

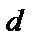 )
)


 для вычисления
для вычисления  )
)
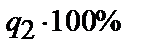
 для случайной величины, имеющей
для случайной величины, имеющей степенями свободы).
степенями свободы).


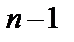



 , где
, где  .
. ;
; ;
; ;
; ;
;



 ,
,