Основные геодезические задачи: вычисление дирекционных угла направлений; решение треугольников; прямая и обратная геодезические задачи.
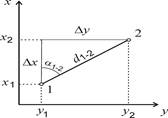
1 Основные геодезические задачи: вычисление дирекционных угла в направлений; решение треугольников; прямая и обратная геодезические задачи. 2 Опорные геодезические сети Основные геодезические задачи: вычисление дирекционных угла направлений; решение треугольников; прямая и обратная геодезические задачи. Определение углов ориентирования. Дирекционный угол направления отрезка на карте измеряют транспортиром как угол, отсчитываемый по направлению часовой стрелки от северного направления линии километровой сетки до направления отрезка. При необходимости перед измерением отрезок удлиняют до пересечения с линией сетки. Для определения азимута А направления сначала измеряют его дирекционный угол a. Затем вычисляют азимут: А =a+g (3.1), где g - сближение меридианов, значение которого подписано под южной рамкой карты и показано на помещённой там же схеме. Можно азимут измерить и непосредственно. Через одноименные значения минут долготы проводят вертикальную линию - меридиан. Угол между северным направлением меридиана и направлением отрезка и есть азимут. Под южной рамкой карты и на схеме указано также склонение магнитной стрелки d, позволяющее вычислить магнитный азимут направления по формуле: А м = А- d (3.2) Прямая и обратная геодезические задачи на плоскости. При вычислительной обработке выполненных на местности измерений, а также при проектировании инженерных сооружений и расчетах для перенесения проектов в натуру возникает необходимость решения прямой и обратной геодезических задач. Прямая геодезическая задача. По известным координатам х 1 и у 1 точки 1, дирекционному углу a1-2 и расстоянию d 1-2 до точки 2 требуется вычислить ее координаты х 2, у 2.
где D х, D у - приращения координат, равные
Обратная геодезическая задача. По известным координатам х 1, у 1 точки 1 и х 2, у 2 точки 2 требуется вычислить расстояние между ними d 1-2 и дирекционный угол a1-2. Из формул (3.4) и рис. 1.1 видно, что
Для определения дирекционного угла a1-2 воспользуемся функцией арктангенса. При этом учтем, что компьютерные программы и микрокалькуляторы выдают главное значение арктангенса w = лежащее в диапазоне -90°£w£+90°, тогда как искомый дирекционный угол a может иметь любое значение в диапазоне 0°£ a £ 360°. Формула перехода от w к a зависит от координатной четверти, в которой расположено заданное направление или, другими словами, от знаков разностей D y = y 2 - y 1 и D x = х 2 - х 1(см. таблицу 3.1 и рис. 3.6). Таблица 3.1
Рис. 1.2. Дирекционные углы и главные значения арктангенса в I, II, III и IV четвертях
Расстояние между точками вычисляют по формуле
или другим путем – по формулам
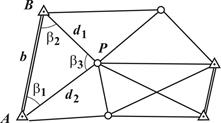
Программами решения прямых и обратных геодезических задач снабжены, в частности, электронные тахеометры, что дает возможность непосредственно в ходе полевых измерений определять координаты наблюдаемых точек, вычислять углы и расстояния для разбивочных работ. 2Опорные геодезические сети Геодезической сетью называют совокупность пунктов на земной поверхности, закрепленных специальными центрами, положение которых определено в общей для них системе координат и высот. Различают плановые, высотные и пространственные сети. Плановые сети – это такие, в которых определены плановые координаты (плоские - x, y или геодезические - широта B и долгота L) пунктов. В высотных сетях определяют высоты пунктов относительно отсчетной поверхности, например, поверхности геоида (а точнее - квазигеоида). В пространственных сетях определяют пространственные координаты пунктов, например, прямоугольные геоцентрические X, Y, Z или геодезические B, L, H. Методы построения плановых сетей: При построении плановых сетей отдельные пункты сети служат исходными – их координаты должны быть известны. Координаты остальных пунктов определяют с помощью измерений, связывающих их с исходными. Плановые геодезические сети создают следующими методами. Триангуляция – метод определения планового положения геодезических пунктов путем построения на местности сети треугольников, в которых измеряют углы, а также длины некоторых сторон, называемых базисными сторонами (рис. 6.1). Положим, что в треугольнике АВP известны координаты пунктов А (
Рис. 2.1. Схема сети триангуляции Продолжая подобным образом, вычисляют длины всех сторон сети. Если, кроме базиса b известны другие базисы (на рис. 6.1 базисы показаны двойной линией), то длины сторон сети можно вычислить с контролем. Дирекционные углы сторон АP и ВP треугольника АВP равны
Координаты пункта P определятся по формулам прямой геодезической задачи
Аналогично вычисляют координаты всех остальных пунктов. Трилатерация – метод определения планового положения геодезических пунктов путем построения на местности сети треугольников, в которых измеряют длины их сторон. Если в треугольнике АВP (рис. 6.1) известен базис b и измерены стороны
Так же вычисляют углы всех треугольников, а затем, как и в триангуляции, - координаты всех пунктов. Линейно-угловая сеть строится, как правило, как сеть треугольников, в которых измеряют углы и длины сторон. Такие сети имеют большое число избыточных измерений и поэтому отличаются высокой надежностью. Полигонометрия – метод определения планового положения геодезических пунктов путем проложения ломаной линии (полигонометрического хода) или системы связанных между собой ломаных линий (сети полигонометрии), в которых измеряют углы поворота и длины сторон.
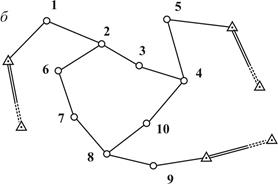
Схема полигонометрического хода показана на рис. 6.2 a, где A и B – исходные пункты; CA и BD - исходные направления, дирекционные углы которых известны; 1, 2, 3, 4, 5- точки (вершины) хода; На рис. 6.2 б показана схема системы полигонометрических ходов. Точки 2, 4, 8, где соединяются разные ходы, называются узловыми. Спутниковый метод определения координат геодезических пунктов основан на измерениях по сигналам спутников навигационных систем ГЛОНАСС (Россия) и GPS (США), выполняемых двумя (и более) наземными приемниками. По результатам измерений с высокой точностью определяют разности Основные виды плановых геодезических сетей: Геодезические сети по назначению классифицируют на государственные геодезические сети, геодезические сети сгущения, геодезические сети специального назначения и съемочные сети.
|

 (3.3)
(3.3)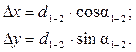 (3.4)
(3.4) . (3.5)
. (3.5)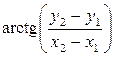 , (3.6)
, (3.6)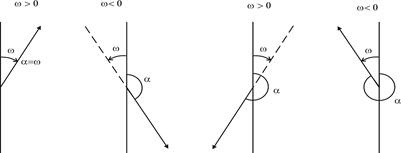
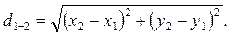 (3.7)
(3.7)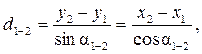
 (3.8)
(3.8)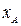 ,
, 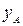 ) и B (
) и B ( ,
, 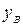 ). Это позволяет путем решения обратной геодезической задачи определить длину стороны
). Это позволяет путем решения обратной геодезической задачи определить длину стороны 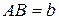 и дирекционный угол
и дирекционный угол  направления с пункта A на пункт B. Длины двух других сторон треугольника АВP могут быть вычислены по теореме синусов
направления с пункта A на пункт B. Длины двух других сторон треугольника АВP могут быть вычислены по теореме синусов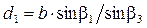 ;
; 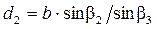 .
.
 ;
; 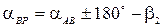 .
.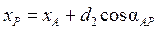 ;
; 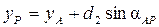 .
.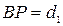 и
и 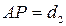 , то на основе теоремы косинусов, можно вычислить углы треугольника;
, то на основе теоремы косинусов, можно вычислить углы треугольника; ;
; ;
; . (6.1)
. (6.1)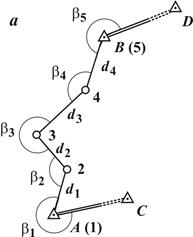
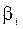 - измеренные горизонтальные углы;
- измеренные горизонтальные углы; 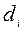 - измеренные длины сторон (i = 1, 2, …).
- измеренные длины сторон (i = 1, 2, …).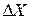 ,
, 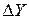 ,
, 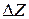 геоцентрических координат между пунктами. Если координаты одного из пунктов известны, то, прибавив к ним измеренные разности, находят координаты остальных пунктов. Затем координаты преобразуют в геодезические или плоские прямоугольные.
геоцентрических координат между пунктами. Если координаты одного из пунктов известны, то, прибавив к ним измеренные разности, находят координаты остальных пунктов. Затем координаты преобразуют в геодезические или плоские прямоугольные.


