Больцмановский отжигИсторически первой схемой метода отжига является так называемая схема Больцмановского отжига. Именно эта схема использовалась Н. Метрополисом для вычисления многомерных интегралов пути в задачах статистической физики, а также С. Киркпатриком для решения задачи нахождения оптимальной разводки микросхем. В Больцмановском отжиге изменение температуры задается формулой:
Вероятностное распределение математическим ожиданием
где Пространство состояний предполагается метрическим. Для Больцмановской схемы доказано, что при достаточно больших
Рис. — Плотность нормального распределения Отжиг Коши (быстрый отжиг) Основным недостатком Больцмановского отжига является медленное убывание температуры. Ввиду этого Цу и Хартли предложили алгоритм, позволяющий использовать для изменения температуры схему
без потери гарантии нахождения глобального минимума. Это достигается за счет использования в качестве
соответствующим образом нормированных. В случае D = 1 приходим к плотности
К сожалению, это распределение не очень удобно моделировать в пространстве размерности больше 1. Этого можно избежать, например, с помощью перемножения
но в этом случае нахождении глобального минимума гарантируется только при законе изменения температуры не быстрее чем:
что гораздо медленнее схемы.
|
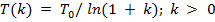
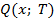выбирается как нормальное распределение (рис.) с
и дисперсией 
, то есть задается плотностью: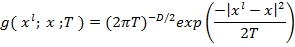
— размерность пространства состояний.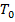
и общем количестве шагов 
, выбор такого семейства распределений гарантирует нахождение глобального минимума.
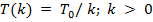
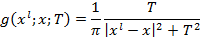
одномерных распределений Коши:
