Алгоритм Ксин Яо
Алгоритм Ксин Яо был повторным применением идеи предыдущего алгоритма. В качестве
Утверждается, что при изменении температуры по закону
достигается статистическая гарантия нахождения глобального минимума. Однако, как показано, увеличение скорости убывания температуры вовсе не означает ускорения в решении задачи. Более того, “размазанность” распределения приводит к тому, что метод генерирует огромное число “длинных” переходов, которые отвергаются в силу низкой вероятности их принятия. Таким образом, несмотря на то, что этот процесс можно итерировать до бесконечности, получая законы изменения температуры вроде
ценность таких “улучшений” представляется сомнительной. Более того, легко видеть, что в пределе это приводит к тривиальному методу случайного поиска, которым является метод отжига при
Методы “тушения” Далеко не всегда хватает вычислительных ресурсов на поиск глобального минимума. Кроме того, зачастую достаточно достигнуть не глобального оптимального решения задачи, а достаточно близкого к нему. Методы “тушения” не гарантируют нахождения глобального минимума, но, как правило, быстро находят близкое решение, а на практике зачастую и сам оптимум. Основная идея этих методов заключается в том, чтобы скомбинировать семейство распределений Например, можно рассматривать нормальное распределение Как правило, в этом случае
|
выбирается
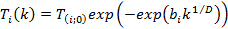
. Это в небольшой степени применимо и к методу сверхбыстрого отжига, так что вопрос о скорости сходимости этих методов, а также о других методах, обеспечивающих не такое быстрое убывание температуры, но большую скорость сходимости, остается открытым. Вполне возможны задачи, на которых вторая итерация вышеописанного процесса может давать не плохие результаты.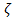
одного из предыдущих четырех методов с более быстрым законом убывания температуры.
из Больцмановского отжига, но при этом уменьшать температуру по закону 
.
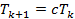выбирается между 0.7 и 0.99. Такой метод очень быстро сходится, и для конкретных задач может давать весьма неплохое решение, близкое к оптимальному, в условиях реального времени. Зачастую они основаны либо на нормальном распределении, либо на распределении для сверхбыстрого отжига. Кроме того, встречаются специальные распределения, подобранные опытным путем для решения конкретных задач.
